Using the Pythagorean Identities .............................

Verifying Identities

sin²θ + cos²θ = 1
sin²θ = 1 - cos²θ
cos²θ = 1 - sin²θ

tan²θ + 1 = sec²θ
tan²θ = sec²θ - 1
sec²θ - tan²θ = 1

1 + cot²θ = csc²θ
cot²θ = csc²θ - 1
csc²θ - cot²θ = 1

Verifying (Proving) Identities

Example 5:

Verify: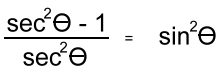

'Verify' means to show that it's true, algebraically.
When possible, start with the more complicated side and try to reduce it to the other side.

We'll start with the left side: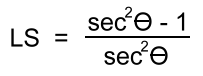

The top is a Pythagorean identity: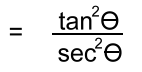

Change everything to sin's and cos's: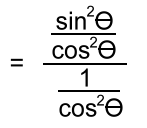

Invert, multiply and simplify.
The result is the same as the right side, which verifies the identity.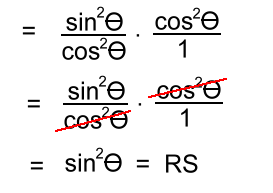

Example 6:

Verify: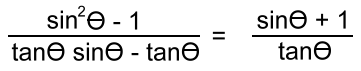

Start with the left side: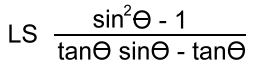

Notice that the top factors as a difference of squares,
as suggested by the top of the right side.
The bottom has a common factor: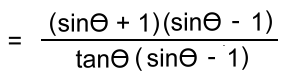

Now simplify, and you're done!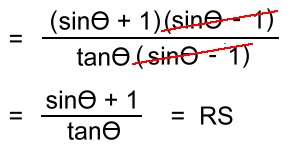

Intro | Simplifying | More Simplifying | Verifying

Resources

Content, HTML & design by Bill Willis 2024