 The results of your three experiments were as follows:
This would lead us to expect that in any equation that will predict the period of a pendulum, there should be a variable for the length of the string, but neither mass nor angle will be involved. Is there anything else that we didn't test, that might affect how fast a pendulum swings? Something that could make it fall faster, for example? There is, but it's not easy to test with simple apparatus. The force of gravity can affect how fast something falls ... if the force is larger, an object will fall faster. You may know that the force of gravity is different on other planets, depending on how large and massive they are. On the moon, for example, the gravity is only a sixth of what it is on Earth, so falling objects (and pendulums) would fall more slowly. Similarly, on Jupiter, where the force of gravity is much larger than on Earth, falling objects (and pendulums) would fall much more quickly. Even on Earth, the force of gravity is not the same everywhere. The farther you are from the centre of the Earth, the smaller the force (and your weight). So you would weigh less while flying (you're high), or more at the North Pole (since the Earth is slightly wider than it is tall). Similarly, if you are standing in a place below which there is a very dense mineral deposit, the force of gravity (and your weight) will be larger. Alternately, if you are standing in a place below which there is a low density pocket, like an oil deposit, the force of gravity (and your weight) will be smaller. In all cases just mentioned, the difference in your weight is so small as to be unnoticeable. But with very accurate instruments, scientists can measure the strength of gravity at various places on Earth to help determine what's below the ground. Because the force of gravity will affect how quickly a pendulum falls, there must be a component of the equation allowing for this. A measure of how quickly things fall is the acceleration due to gravity, g, and this is included in the equation as well. An average value for g on Earth is about 9.81 m/s2, but it varies slightly from place to place. The larger its value, the shorter the period, so it's an inverse relationship. Here's the equation that will allow you to work out the period of a pendulum: 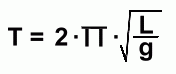 Notice that the period T depends on the length of the pendulum directly. As L gets larger, so will T. On the other hand, g is on the bottom, so as it gets bigger, the period T will get shorter. If gravity is larger, it falls faster. This isn't a linear relation, since there is a square root in the equation. But you'll notice that there are no variables for mass or angle, since the period is not affected by changing these. If you use units m/s2 for g, and metres for length L, then the period units will be seconds If you square both sides of the equation and rearrange it, you can solve for L: 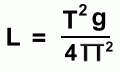 This will let you calculate the length of a pendulum if you know its period. 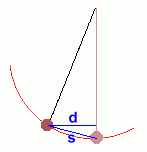 To be more accurate, we should mention that the angle of the release does not matter,as long as the following condition applies: The angle to which you pull the pendulum mass, and the length of the string, should be values such that the mass's displacement from rest position (s) and its horizontal displacement (d) are of roughly the same size. For short pendulums, this means the angle should be small. As long as this is true, the angle won't affect the period, and the equations can be used. Other equations describing a pendulum's motion can be derived using potential and kinetic energy relationships. To learn more about this, go on to the next page. |