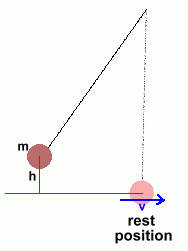
When the mass on the pendulum is pulled back to some angle, it is above the rest level. This gives it additional potential energy  EP, which can be measured using the equation EP = m · g · h  h  is the height of mass  m  above rest position, and  g   is the acceleration of gravity. When the mass passes through the lowest point, it is moving with velocity  v, and all of its potential energy has been converted to kinetic energy (ignoring friction losses). The kinetic energy  EK is given by: EK = 0.5 m · v2 Since these energies are equal, we can set one equation equal to the other, and see what we can solve for. This will give us some useful new formulas. Since  EK equals  EP as the pendulum passes through rest position: We can reaarange and solve for the velocity  v: This gives a way to calculate the velocity of a pendulum mass as it passes through its rest position. You need only know the vertical height above rest from which you dropped it, and  g. Alternately, we could solve the equation for  g: 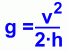This gives us a way to measure the value of  g, which, as you remember from the previous page, is not really constant. All we need to do is set up a pendulum and measure its velocity as it passes through the rest point, after releasing it from a height  h above that point. This equation could be used to confirm that  g is about 9.8 m/s2 on Earth. It could also be used on another planet to work out the value of  g  there. But you probably couldn't use this to measure changes in  g  from place to place on Earth, without accurate measuring devices. You might also like to learn about conservation of momentum using a pendulum. Pendulum Experiment | Variables | Experiment 1 | Experiment 2 | Experiment 3 | Equation pg 1 Resources