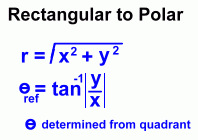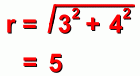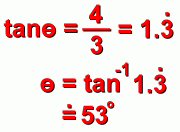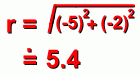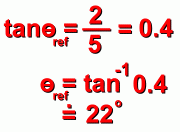
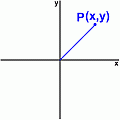
The method you first used to identify point P on a set of axes was the Cartesian coordinate system. Every point on the grid can be located using a unique pair of numbers (x, y) describing its position.

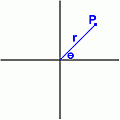
Another way to locate point P, called the polar coordinate system, is by specifying its distance from the origin along radius r, and the angle from zero of this radius. Every point is specified by a unique pair of numbers (r, ).

This page will give examples of each method, and show you how to convert a given point's coordinates from one system to the other and back.
All of the mathematics used here should be familiar to you.

Converting Rectangular Coordinates to Polar


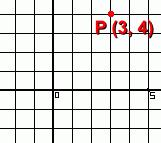
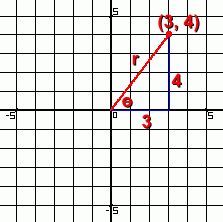
Here is a point that we have located using the Cartesian, or rectangular coordinate system.

Let's convert this to polar coordinates.
We'll need to calculate the values of
both  r and  .


r  is the distance to the point from the origin. It's always positive.
 is the angle to the radius line, from the positive x-axis.

r is calculated using the Pythagorean Theorem:


 is calculated using trigonometry, by solving the tan fraction for the angle:

So the point  (3, 4) in rectangular coordinates is equivalent to the polar form  (5, 53°)



Let's look at another example of converting rectangular coordinates to polar, but this time we'll use a point that is not in the first quadrant.


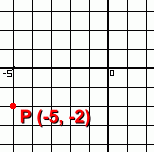
Here is a point that we have located using the rectangular coordinate system.
It's in quadrant 3.

Let's convert this to polar coordinates.
We'll need to calculate the values of
both  r and  .


r  is the distance to the point from the origin. It's always positive.
 is the angle to the radius line, from the positive x-axis.

r is again calculated using the Pythagorean Theorem:


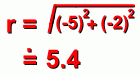
 is calculated by first finding the reference angle, using the positive (or absolute) values of  y and  x, and solving the tan fraction for the reference angle:




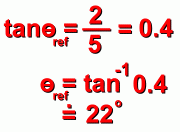
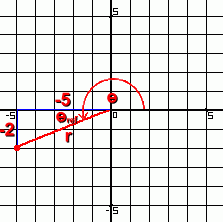
The value of   is then determined by using the diagram and noting which quadrant it's in.
In this case,   must be 180° plus another 22°, or  202°

So the point  (-5, -2) is equivalent to the polar form  (5.4, 202°)




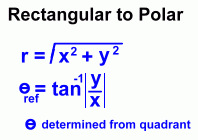
Summary:

When converting rectangular coordinates to polar coordinates, you can find the values of  r and   using the methods shown at the right.


Now let's look at how to convert polar coordinates to rectangular ones.
Go on to  page two >>



Resources


Conent, HTML, graphics & design by Bill Willis 2023