 Page Two Rectangle and Square Base Pyramids: Surface Area We'll have to distinguish between square base and rectangle base pyramids, because the methods for finding the surface area are different.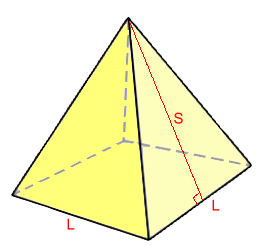 
Square Base PyramidsThe surface area is made of a square base (area = L·L) and four identical triangles (A = b·h/2) around the sides. We will need to know the height of each of these triangles, which is also the slant height S of the pyramid. S.A. = L ·L + 4(L·S ÷ 2) S.A. = L2 + 2L·S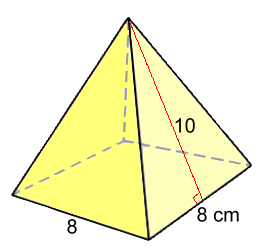 
Example 5: Find the surface areaS.A. = L2 + 2L·S S.A. = 82 + 2(8)(10) S.A. = 224 cm2 Note the use of brackets to show substituted numbers that are multiplied. If we know the height of the pyramid but not the slant height, we'll need to solve for S first: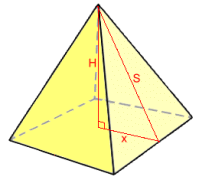 
Given height H and half the base side x Using the Pythagorean Theorem: S2 = H2 + x2 Example 6: Find the surface area rounded to 2 d.p.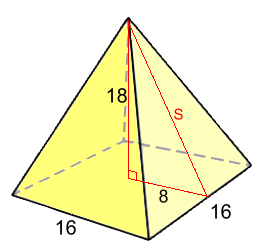 
We don't know S, so we'll need to calculate it first:S2 = 182 + 82 S ≈ 19.698 Now find the surface area: S.A. = L2 + 2L·S S.A. ≈ 162 + 2(16)(19.698) S.A. ≈ 886.34 cm2 S can also be calculated if you're given the edge length of the pyramid. We won't show one of those.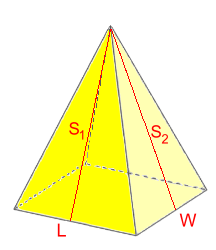 
Rectangle Base PyramidsThe complication here is that the triangular faces are different; there are two pairs of different triangular sides. S.A. = L·W + 2(L·S1÷2) + 2(W·S2÷2) S.A. = L·W + L·S1 + W·S2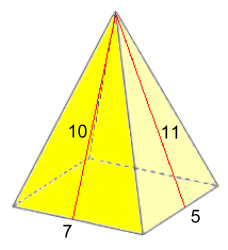 
Example 7: Find the surface areaS.A. = L·W + L·S1 + W·S2 S.A. = 7·5 + 7·10 + 5·11 S.A. = 160 cm2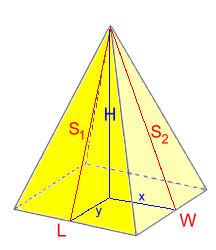 
If we know the height of the pyramid but not the two different slant heights, we'll have to calculate them first, using the Pythagorean Theorem again. S12 = H2 + y2 S22 = H2 + x2 Example 8: Find the surface area rounded to 1 d.p.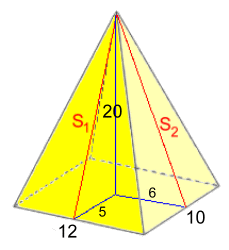 
S12 = 202 + 52S1 ≈ 20.62 S22 = 202 + 62 S2 ≈ 20.89 S.A. = L·W + L·S1 + W·S2 S.A. ≈ 12·10 + 12(20.62) + 10(20.89) S.A. ≈ 576.3 cm2 |