 Rectangle Base Pyramids: Volume 
The volume of a rectangular prism is given by the formula V = L·W·H A rectangle base pyramid has one third of the volume, so its volume is given by the formula V = L·W·H ÷ 3 The height will often be shown inside the pyramid.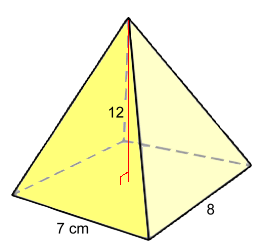 
Example 1: Find the volumeV = L·W·H ÷ 3 V = 7·8·12 ÷ 3 V = 224 cm3 - Which you call length or width doesn't matter. - A square base pyramid would use the same formula.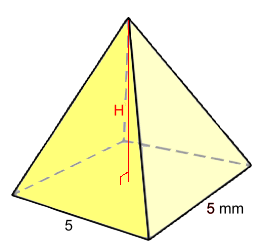 
Example 2: The volume is 410 mm3. Find the height rounded to 1 d.p. V = L·W·H ÷ 3 410 = 5·5·H ÷ 3 410 ≈ 8.33·H 49.2 mm ≈ H We used the convention that says: "for an answer rounded to 1 d.p., carry 2 d.p. until the last step".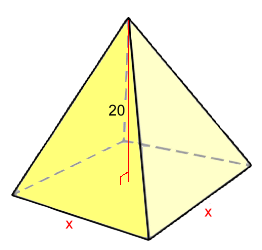 
Example 3: The volume is 711 cm3. Find the sides of the square base. V = L·W·H ÷ 3 711 = x·x·20 ÷ 3 711 ≈ 6.67·x2 106.60 ≈ x2 10.3 cm ≈ x Another common convention is to assume rounding to 1 d.p. if the question doesn't specify. Triangle Base Pyramids: Volume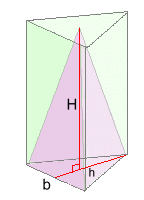 
The volume of a triangular prism is given by the formula V = (b·h ÷ 2)·H A triangle base pyramid has one third of the volume, so its volume is given by the formula V = (b·h ÷ 2)·H ÷ 3 or V = (b·h·H) ÷ 6 Notice the difference between 'H' and 'h'.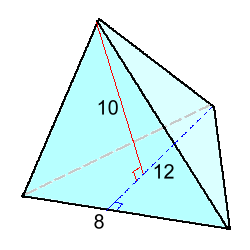 
Example 4: Find the volume V = (b·h·H) ÷ 6 V = 8·12·10 ÷ 6 V = 160 cm3 |