|
The Pythagorean Theorem must work in any 90 degree triangle. This means that if you know two of the sides, you can always find the third one. Example 1: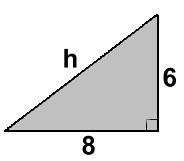 
h2 = 62 + 82 Simplifying the squares gives: h2 = 36 + 64 h2 = 100 h = 10 (by doing the square root of 100) Example 2: Here the missing side is not the long one. But the theorem still works,as long as you start with the hypotenuse: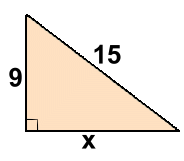 
152 = x2 + 92
225 = x2 + 81 225 - 81 = x2 + 81 - 81 144 = x2 12 = x Example 3: Sometimes the answer will be irrational and will need to be rounded ...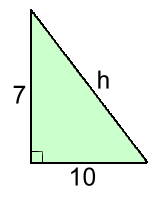 
h2 = 72 + 102 h2 = 49 + 100 h2 = 149 h ≃ 12.2 rounded to 1 d.p. Example 4: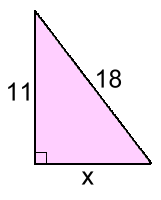 
Again, the missing side isn't the long one, but we start with the hypotenuse:182 = x2 + 112 324 = x2 + 121 203 = x2 x ≃ 14.2 rounded to 1 d.p. Here's a real problem that uses the theorem: "How far up a wall will an 11 foot ladder reach, if the base of the ladder must be 4 feet from the foot of the wall?"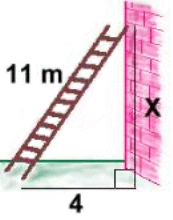 
112 = x2 + 42 121 = x2 + 16 105 = x2 x ≃ 10.2 rounded to 1 d.p. The ladder can reach about 10.2 feet high. Now you're ready for the quiz >>> |