 dividing radicals, you should review radical simplifying. Types of Radicals: 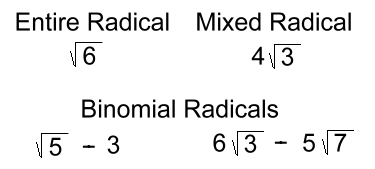
Adding and subtracting radical expressions is similar to operations with polynomials, except that individual radicals themselves can often be simplified after combining. Adding Radical Expressions Example 1: 3√7 + 5√7 + 2√7 = 10√7 Just like combining x's Example 2: (3√2 + 5) + (7√2 - 9) = 3√2 + 5 + 7√2 - 9 with addition, the brackets are superfluous = 10√2 - 4 Combine like terms Example 3: 4√5 + 2√11 + 4 + 8√5 + √11 - 1 = 12√5 + 3√11 + 3 Combine like terms Example 4: 5√12 + 2√27 No like terms, but the radicals will simplify = 5√4√3 + 2√9√3 = 5(2)√3 + 2(3)√3 = 10√3 + 6√3 Now we have like terms to combine = 16√3 Example 5: 3√8 - 5√12 + 2 + 7√32 + 2√75 + 9 Simplify the radicals first = 3√4√2 - 5√4√3 + 2 + 7√16√2 + 2√25√3 + 9 = 3(2)√2 - 5(2)√3 + 2 + 7(4)√2 + 2(5)√3 + 9 = 6√2 - 10√3 + 2 + 28√2 + 10√3 + 9 Combine the like terms = 34√2 + 11 The √3 terms added to zero Subtracting Radical Expressions The only difference here is that any brackets in the expression will result in an additional step where we switch signs. Example 6: (4√45 - 2√8 + 5) - (3√20 + 3√18 - 11) = 4√45 - 2√8 + 5 - 3√20 - 3√18 + 11 Signs in the second bracket were switched = 4√9√5 - 2√4√2 + 5 - 3√4√5 - 3√9√2 + 11 Simplify the radicals = 4(3)√5 - 2(2)C2 + 5 - 3(2)√5 - 3(3)√2 + 11 = 12√5 - 4√2 + 5 - 6√5 - 9√2 + 11 Now combine likee terms = 6√5 - 13√2 + 16 Example 7: (√6 - 4) - (3√6 + 5) + (8√6 - 1) = √6 - 4 - 3√6 - 5 + 8√6 - 1 Only the middle bracket had the signs switched = 6√6 - 10 Now let's look at multiplying radical expressions >>> |