 Page Three Rationalizing a Binomial Denominator Before we try some actual examples, we'll need to practice multiplying radical binomials. Here is an example of a binomial containing radicals: In order to remove the radicals, we will need to multiply this expression by its conjugate. The conjugate of a binomial is the same binomial with the sign in the middle switched. The conjugate of the binomial above would be Watch what happens when we multiply them together: We'll need to use the FOIL method: 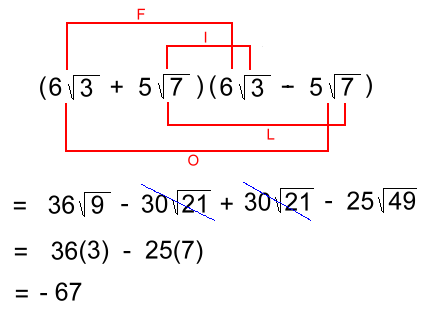
The first and last multiplications result in whole numbers. The ouside and inside multiplications result in terms which add to 0. The result is a rational number (no irrational radicals) This procedure should look familiar, as it mimics the multiplication of binomials that result in a binomial called a difference of squares. We'll also need to be able to multiply two binomials that aren't conjugates. Our second example will be a little more work. Can you see why? 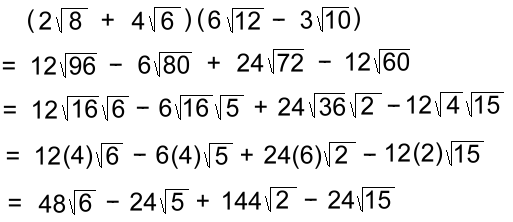
Not only do the two middle terms not disappear, but the larger numbers make simplifying the radicals more challenging. If some of the final terms had had the same radicals, we would have had an additional step where we'd combine like terms. OK, now we're ready to learn how to rationalize expressions with binomial denominators. Move on to page 3b >>> |