 Rationalizing the denominators of answers is an additional step in simplfying, where answers contain radicals in the denominator. The aim is to make an expression easier to evaluate by eliminating the need to divide by irrational (radical) terms. This need has been made largely irrelevant with the use of advanced calculators, but the requirement that denominators be rationalized is still a part of high school math curricula. 'Rationalizing' means turning an irrational radical into a rational number. We'll look at two types: 1. The denominator is a single term containing a single radical or mixed radical 2. The denominator is a binomial containing radicals [We will assume that you are proficient in radical operations and simplifying square roots.] Type 1: Denominator a Single or Mixed Radical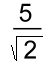 
Here's an example. This could be the answer to a problem, but the denominator is an irrational radical. We want to change this expression so that the denominator is no longer irrational. Here's how we'll do it.
We're going to use the fact that when you multiply a radical by itself, the radical sign disappears:  Another way to describe what's happening here is to say that when you multiply a radical by itself, the result is the 'radicand', or what was under the radical sign:  Whichever way you look at it, the result of doing this is to get rid of the radical sign. Let's return to the example: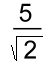
If we're going to remove the radical sign in the denominator by multiplying by √2, we'll need to do it to the top also; we want to multiply the fraction by something that is equivalent to 1, so that the fraction's value does not change.
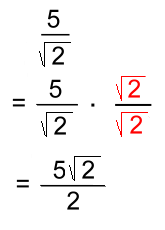 Multiplying top and bottom by √2 won't change the value of the expression, but will remove the radical in the denominator. Notice that the answer is more complicated than the original expression: 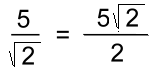 Nevertheless, the answer is considered to be simpler because the denominator no longer contains an irrational radical. Here's another example: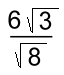 
We'll multiply top and bottom by √8: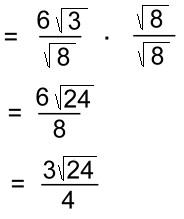 
and simplify. But now we discover that the radical on top can be simplified: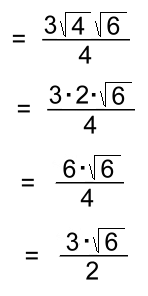 
The final answer. Here's one where the denominator is a mixed radical. 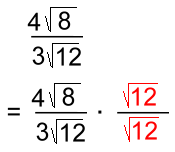 With just one term in the denominator, we only have to multiply top and bottom by the radical √12, without the 3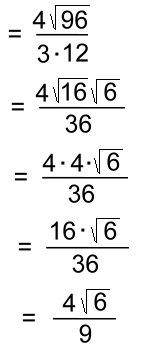 
Here's the rest of the simplifying. Notice that we're simplifying the √96 early, to save a step or two. The whole number fraction can be reduced independently of the radical. The final answer. These questions can be rather lengthy to answer. Before looking at binomial denominators, let's examine some shortcuts to watch out for, to reduce the amount of work we have to do. Move on to page two >>> |