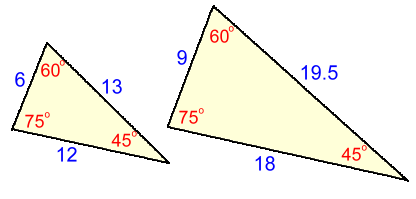
 
Unlike congruent triangles which are identical in size and shape, similar triangles are not the same size, but they do have the same shape.This is because: - corresponding angles are the same - corresponding sides are in the same ratio In this example, the sides of the large triangle are all 1.5 times as long as the sides of the small one. The fact that the sides are in the same ratio can be used to solve for missing information in a problem. For example: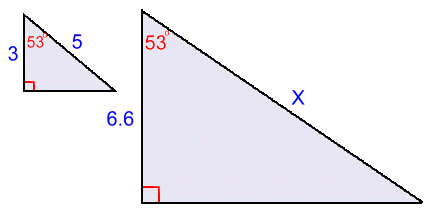 
We know that the triangles are similar because all three pairs of correxponding angles are equal. (The diagram doesn't have to label the third pair; if two corresponding angles are equal, the third pair must be too. Here they would be 37°). This means corresponding sides must be in the same ratio. We can use this to find side x. x must equal 6.6 5 3 x = 6.6 5 3 Cross multiply: 3x = 33 x = 11 This method can be used to solve practical problems: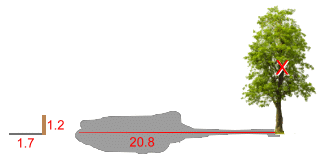 
A tree casts a 20.8 m shadow.A 1.2 m tall stick placed on the ground casts a 1.7 m shadow. How tall is the tree?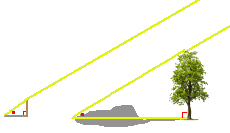 
The angle to the Sun is the same, so the two triangles we can draw will have the same angles, so are similar.Below is the solution where we solve for x, the height of the tree: 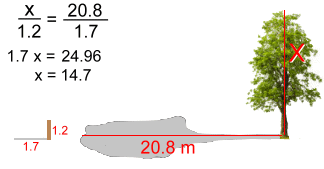 The height of the tree is 14.7 metres. to find the height of a building ... see method #11 |