 Most trigonometric values are irrational numbers which, when used in calculations. require that the answer be rounded. There are occasions, however, when we would like an exact answer, rather than a rounded one. Some trig values are exact. For example, cos60° is 0.5, and tan45° is 1. What is needed is an easy way to know which angles yield exact values for the trig ratios, and what those values are. That's the purpose of the so-called 'special triangles': triangles with known sides and angles that are easy to remember, and which allow you to make fractions for all the trig functions of some angles without having to round a decimal. Some fractions will include radicals like √2; as long as we don't evaluate them, we won't have to round. There are two special triangles that will let you make trig fractions for three different angles: 30°, 45°, and 60°.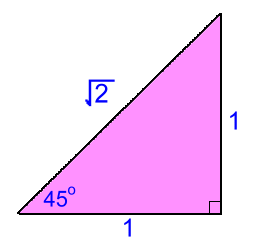 
This first right triangle has a 45° angle in the corner. Using the definitions of the trig fractions, recalled using the acronym 'SOHCAHTOA', we can write the six basic trig fractions:sin45 = 1/√2 csc45 = √2/1 = √2 cos45 = 1/√2 sec45 = √2/1 = √2 tan45 = 1/1 = 1 cot45 = 1/1 = 1 [The other angle is also 45°, so it would give the same values]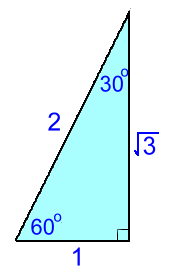 
The second right triangle has angles 60° and 30°.Using the 60° angle: sin60 = √3/2 csc60 = 2/√3 cos60 = 1/2 sec60 = 2/1 = 2 tan60 = √3/1 = √3 cot60 = 1/√3 Using the 30° angle at the top: sin30 = 1/2 csc30 = 2/1 = 2 cos30 = √3/2 sec60 = 2/√3 tan30 = 1/√3 cot30 = √3/1 = √3 Some textbooks will give rationalized values for these trig fractions, but there isn't much point in that as the exact values are often used in calculations that get simplified and rationalized anyway. There are many more angles we can find exact trig fractions for, based on these three. Any angle on an x-y grid whose reference angle is 30, 45, or 60, for example, will let you use the CAST rule and the triangles above to get exact trig fractions. For instance, cos150° = -cos30 = -√3/2 Trigonometric identities let you find exact values for other angles. For example: cos75° = cos(45+30) = cos45·cos30 - sin45·sin30 = (1/√2)(√3/2) - (1/√2)(1/2) = (√3/2√2) - (1/2√2) = (√3 - 1)/2√2 |