The surface area of a three dimensional object is the total area of all of its faces. Lets look at some examples and we'll show you several ways to find the surface area. Rectangular Prisms 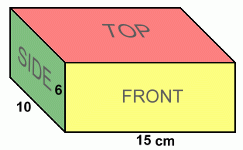Pictured on the right is a right rectangular prism. It's a prism because all of the faces are flat, and there are two ends. It's called a rectangular prism because all of the faces are rectangles; it's also a right prism because the angles between all the faces are 90°. Since all of the prisms we look at in high school mathematics are right prisms, we'll leave out the word 'right' from now on. In order to calculate its total surface area, you first have to realize that this figure has six faces. At the moment you can only see three of them. Let's redraw the figure so that it is transparent. This will allow us to see all six of the faces. 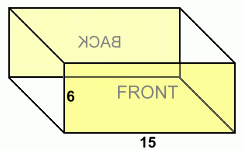Here are the front and the back. These two faces are identical in size. Each of these two faces is a rectangle. You already know how to calculate the area of a rectangle: the formula for a rectangle's area is given by A = L · W Front area =  L · W  =  15 · 6  =  90 cm2 Back area  =  L · W  =  15 · 6  =  90 cm2 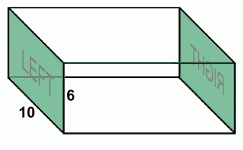Here are the left and the right. These two faces are identical. Each of these two faces is a rectangle. Left area  =   L · W   =  10 · 6  =  60 cm2 Right area  =  L · W  =  10 · 6  =  60 cm2 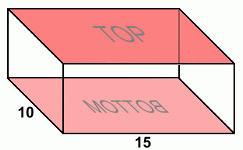Here are the top and bottom. These two faces are identical. Each of these two faces is a rectangle. Top area   =     L · W  =   15 · 10  =  150 cm2 Bottom area =  L · W  =  15 · 10  =  150 cm2 Now the total surface area of the figure can be found by adding the areas of all six faces:        Surface Area = 90 + 90 + 60 + 60 + 150 + 150 = 600 cm2 You may have noticed that for the three area calculations above (each one of which is doubled up), the numbers used for the length and width were just the three measurements of the prism, taken in pairs. If you can see how this works, and would like a quicker way to calculate the surface area of a rectangular prism, here's a formula that always works, and will give you the answer in one step: Surface Area of a Rectangular Prism  =  2·L·W  +  2·L·H  +  2·W·H S. A. = 2·15·10  +  2·15·6  +  2·10· 6          = 600 cm2 ... where L, W, and H are the length, width and height of the prism. Make sure your teacher will allow you to use this formula for your work; in grade 7/8 classes you may be asked to calculate surface area step-by-step instead, like we did at the top of the page.        Now let's do another example with a different kind of prism ... Main Page