 Triangular Prisms 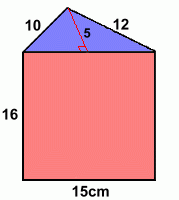
At the left is a triangular prism. It's different from a rectangular prism in several ways: - The ends are triangles (that's why it's a triangular prism) - There are only five sides altogether - The rectangular sides aren't all the same (at least in this example) To find the total surface are, we'll have to find the areas of the three rectangular faces, the areas of the top and bottom (these are the same), and then add all five areas together. Like we did before, we'll redraw the shape transparent to make it easier to see the faces we'll be calculationg the areas for. 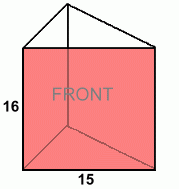
Here is the front face. It's a rectangle. Front area = L · W = 16 · 15 = 240 cm2 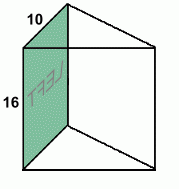
Here is the left face. It's a rectangle. Left area = L · W = 16 · 10 = 160 cm2 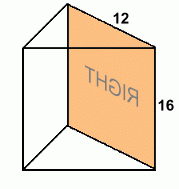
Here is the right face. It's a rectangle. Right area = L · W = 16 · 12 = 192 cm2 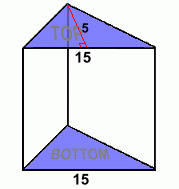
Here are the top and the bottom. These two faces are identical in size. Each of these two faces is a triangle. You already know how to calculate the area of a triangle: the formula is given by A = (b · h)/2 Top area = (15 · 5) / 2 = 75 / 2 = 37.5 cm2 Bottom area = (15 · 5) / 2 = 75 / 2 = 37.5 cm2 Now the total surface area of the figure can be found by adding the areas of all five faces: Surface Area = 240 + 160 + 192 + 60 + 37.5 + 37.5 = 667 cm2 Now let's do another example with a cylinder ... |