Volume of a Triangular Prism 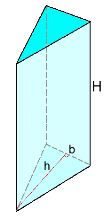As in all prisms, as well as cylinders, the volume is found using the generic formula V= B·H, where B is the area of the base. In triangular prisms the base is a triangle whose area is b·h/2 So for a triangular prism: V = B·H =   (b·h/2) · H    or   V = b·h·H ÷ 2 Note the difference between h and H 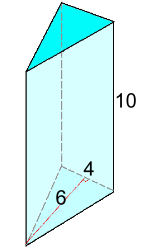Example 1: Find the volume in cm3 V = b·h·H ÷ 2 V = 4·6·10 ÷ 2 V = 120 cm3 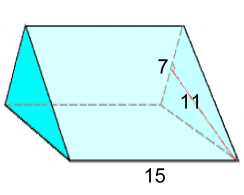Example 2: Find the volume V = b·h·H ÷ 2 V = 7·11·15 ÷ 2 V = 577.5 cm3 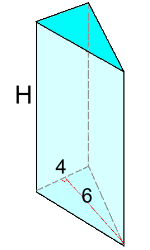Example 3 The volume is 800 mm3. Find the height H. V = b·h·H ÷ 2 800 = 4·6·H ÷ 2 800 = 12·H 66.7 mm ≈ H Surface Area of a Triangular Prism 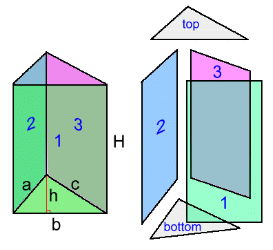The surface area is composed of two identical triangles on top and bottom: A = b·h/2 for each. There are also three different rectangles 1, 2, & 3 around the sides, with areas  b·H,  a·H   and  c·H Rather than a formula, most people find the surface area by finding the individual side areas: top, bottom (the same), left side, right side, and front (or some other designations, depending on the orientation). Example 4: Find the surface area 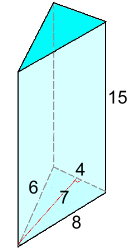Bottom: A = b·h/2 = 4·7/2 = 14 Top: (same) A = 14 L.S.: A = 15·6 = 90 R.S.: A = 15·8 = 120 Back: A = 15·4 = 60 Total surface area = 298 cm2 Notes: We use dots for multiplication. When the values have decimals, we'll switch to brackets, as in the next example. When the units aren't specified, we assume they're centimetres. Example 5: Find the surface area in mm2 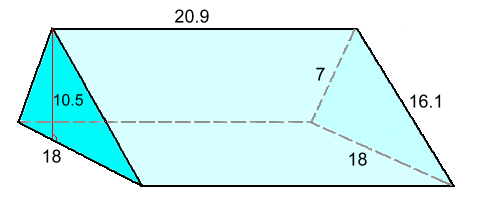Left: A = (18)(10.5)/2 = 94.5 Right: A (same) = 94.5 Back: A = (20.9)(7) = 146.3 Front: A = (20.9)(16.1) = 336.49 Bottom: A = (20.9)(18) = 376.2 Total surface area = 1048.0 mm2 We continue to follow the convention of carrying one extra decimal place until the last step. Example 6: Find the surface area 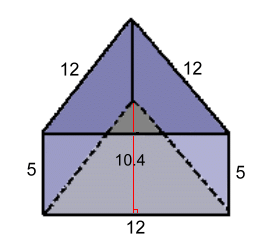Top: A = (12)(10.4)/2 = 62.4 Bottom: A = 62.4 Because the top and bottom are equilateral triangles, the three rectangular sides are the same. L.S.: A = (12)(5) = 60 R.S.: A = 60 Front: A = 60 Total surface area = 304.8 cm2 Resources Content, artwork, HTML & design by Bill Willis 2024