 Page Four In order to do calculations at an angle, you'll have to understand vector components and vector addition.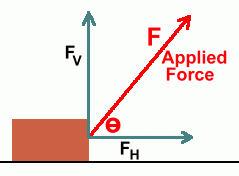 
Here is our 20 kg mass again. This time we're pulling on it in an upwards direction, at the angle shown. The applied force is no longer pulling entirely in a forwards direction; one component pulls up, and another component pulls forwards. The horizontal component of the force, FH, can be used to balance or overcome the frictional force. The vertical component of the force, FV, can be used to lessen the normal force, and thus reduce the frictional force. The size of the components of F can be calculated using these equations:  In practice, questions involving forces at an angle, friction, and acceleration, all in the same question, would be a little too complicated for Physics 20. Instead, you'll see problems like the following: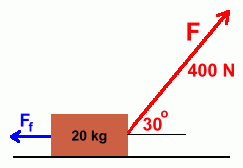 
An object is moving at constant velocity. This velocity is being maintained by a force of 400 N that is pulling on the 20 kg mass at an angle of 30°. What is the force of friction? Because there is no acceleration, the force of friction is exactly balanced by the forward horizontal component of the applied force. Work that out, and you'll know what the frictional force is. FH = F · cos 30 = 400 x cos30 = 346.4 N so the frictional force is -346.4 N. Here's a similar problem. With several forces that are horizontal and vertical, we won't need to use components, but we will have to be able to add vectors. 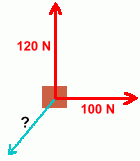 Two people are pulling on an object, with forces of 120 N vertically, and 100 N horizontally.Ignoring friction, at what force and angle must you pull in order to keep the object from moving? This is an 'equilibrium' question. In order to prevent movement, you must pull with a force that is the same size as the sum of the two other vectors, and at an angle 180° in the opposite direction. We'll have to calculate the sum of the forces, and the angle this sum vector makes with the horizontal. 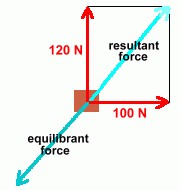 Here's a diagram of what we must do.First we'll have to find the size of the resultant force, which is the vector sum of the two red forces. 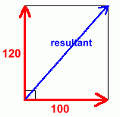 Then we'll have to find the angle this sum vector makes with the horizontal.The final step will be to state the size and direction of the equilibrant. The vector sum diagram is shown at the right. We'll leave the vectors 'tail to tail', and redraw the diagram. 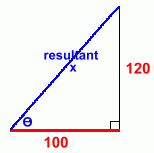 Here is the right triangle we'll need in order to solve for the length of the sum vector (x) and the angle with the horizontal. Using the Pythagorean Theorem, the value of x turns out to be 156.2 m. Using simple trigonometry, the value of the angle works out to be about 50°. You've used both of these methods in Math 9 and Math 10, so we won't show the work.
These pages are not meant to be a complete introduction to forces in Physics 20, nor have we covered every type of problem. In particular, if a pair of forces do not meet at a 90° angle, you will have to find the vector sum using either a scale diagram, the components method, or the sine and cosine laws. Also, we did not show examples involving the parallel and normal components of a force applied to an object on a ramp; however, we do have an illustration of this concept in our Amusement Park Physics section. You should consult your physics textbook or your teacher for help with these topics. |
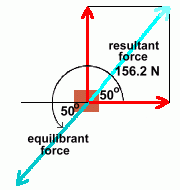Here's the original diagram, with our answers added.