 Page Two 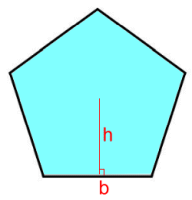 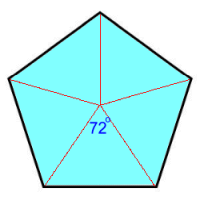 Regular Pentagons All the sides b are the same length. We'll need to calculate height h. We'll split the pentagon into five identical triangles. The central angle in each will be 360°÷2 = 72°. 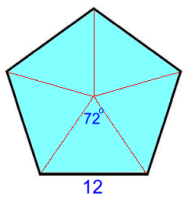 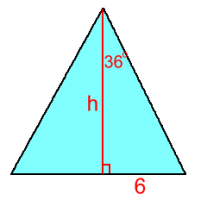 Here's an actual example, with sides 12 cm.Looking at one of the triangles, the height h is marked, along with half the top angle, 36°. 6/h = tan36 h = 6/tan36 So the area of the whole triangle is: A = b·h/2 = 12(6/tan36) ÷ 2 A = 36/tan36 This means the area of the regular pentagon, with five of those triangles, is: A = 5(36/tan36) = 180/tan36 ≈ 247.7 cm2 Let's derive a formula so we'll be able to calculate the area of a regular pentagon in one step: 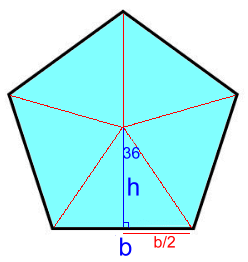 (b/2)/h = tan36 h = (b/2)/tan36 h = b/2·tan36 A (full triangle) = b·h/2 = b[b/2·tan36]/2 A = b2/4·tan36 Regular pentagon area = 5[b2/4·tan36]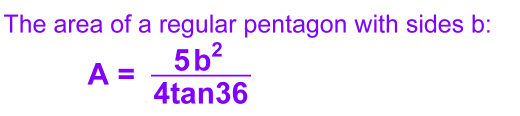 
Let's use the formula to check the answer to the original example above with side 12 cm: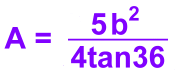 
A = 5(12)2/(4tan36) A ≈ 247.7 cm2 Now let's move on to regular polygons with six sides >>> |