 Page Four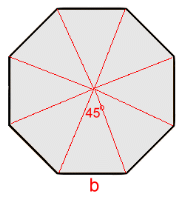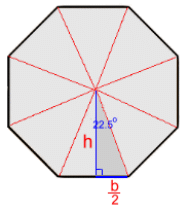  
Regular Octagons Each segment has a top angle of 360÷8 = 45°. To calculate the height, use half the triangle. tan(22.5) = b/2 ÷ h h·tan(22.5) = b/2 h = b/2 ÷ tan(22.5) h = b/[2·tan(22.5)]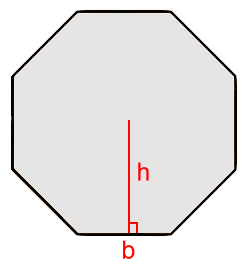 
The area of one triangle: A = b·h / 2 A = b · b/[2·tan(22.5)] / 2 A = b2 / 4·tan(22.5) Area of regular octagon with 8 triangles: A = 8[b2 / 4·tan(22.5)] A = 2b2 / tan(22.5) [Since half-angle trig functions aren't used in high school math, we won't convert this to exact values]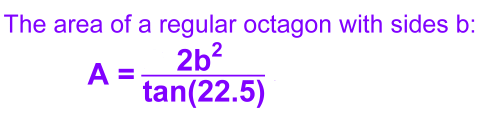 
Let's try an actual example: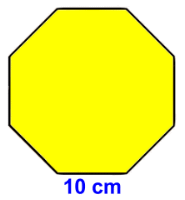 
A regular octagon has side length 10 cm. Find its area. 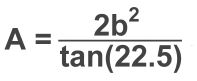A = 2(10)2/tan(22.5) A ≈ 482.8 cm2 |