 Regular polygons are polygons where all the sides are the same length. We'll look at regular triangles, called 'equilateral', regular quadrilaterals, called 'squares', as well as regular pentagons, hexagons, and octagons. The area calculations for all shapes except squares will require some simple trigonometry.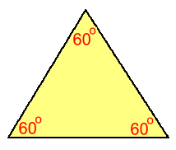 
Regular (Equilateral) Triangles Given the side lengths for the triangle (all the same), we'll need to know the height of the triangle in order to find the area. We'll show this in several steps, with an actual example.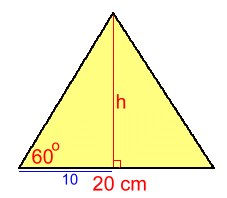 
Here's an equilateral triangle with sides 20 cm. Height h is shown.We can use trigonometry to solve the left triangle for h. h/10 = tan60 h = 10·tan60 ≈ 17.32 Area = b·h/2 A ≈ (20)(17.32)÷2 ≈ 173.2 cm2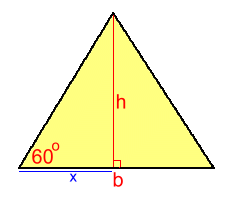 
Let's derive a formula for the area so it can be calculated in one step.x is half the base. tan60 = h/x h = x·tan60 From the special triangle for 60°: tan60 = √3 so h = x·√3 This makes the area: A = b·h/2 and recalling that x is half of the side b: A = b·(√3·x)/2 A = b·(√3·(b/2))/2 A = √3b2/4 Area of a regular (equilateral) triangle with sides b: A = √3b2/4 Let's use the formula to check the answer to the original triangle above with side 20 cm: A = √3b2/4 = √3(20)2/4 ≈ 173.2 cm2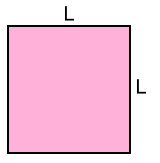 
Regular Quadrilaterals (Squares) This one you've known how to do for years! A = L·L or A = L2 Area of a regular quadrilateral (square) with sides L: A = L2 Now let's move on to regular polygons with five sides >>> |