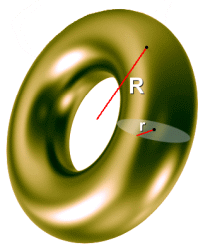
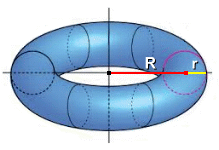
A torus is a 3D shape obtained by revolving a circle around an axis. It's the shape of doughnuts, rings, tires, and inner tubes. A torus has two radii. The first radius, the smaller one, is the radius of the cross-section r. The second radius R is the radius of revolution, which is the distance between the center axis and the center of the cross-section. Both of these measurements are needed to calculate the volume and surface area of a torus.    Surface Area of a Torus   SA = (2πR)·(2πr)   or    SA = 4π2·R·r If you cut and straighten the torus, you would get a cylinder with radius r and height 2πR  (the original torus circumference) SA = 2πr2 + 2πrH  =  2πr(2πR  )  =  4π2·R·r    Volume of a Torus   V = (πr2)(2πR)    or    V = 2π2·R·r2 If you cut and straighten the torus, you would get a cylinder with radius r and height 2πR  (the original torus circumference) V = πr2H  =  πr2(2πR)  =  2π2·R·r2 Let's try some examples: 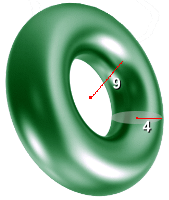Example 1: Inner radius = 4 cm    Large radius = 9 cm V = 2π2·R·r2 = 2π2(9)(42) = 2842.4 cm3 SA = 4π2·R·r = 4π2(9)(4) = 1421.2 cm2 Both calculations can be done in one step on your calculator. 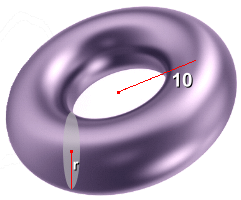Example 2: Outer radius = 10 cm    Volume = 8000 cm3         Find the inner radius r V = 2π2·R·r2 8000 = 2π2·(10)·r2 8000 ÷ (2π2·(10)) = r2     Enter in one step with brackets 40.53 = r2 6.4 cm = r 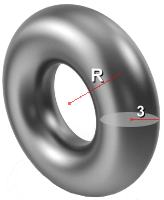Example 3: Inner radius = 3 cm   Surface area = 10,000 cm2   Find R SA = 4π2·R·r 10000 = 4π2·R·3 10000 ÷ (4π2·3) = R     Enter in one step with brackets 84.4 cm = R For Math 31 students (calculus): Here is the derivation of the Volume formula, by integrating Surface Area over r: Volume = ∫ (Surface area) dr V = ∫ (4π2·R·r) dr V = (4π2·R) · ∫ r dr V = (4π2·R) · r2/2 V = 2π2·R·r2 You can also differentiate the Volume formula with respect to r to get Surface Area: SA = d/dr (2π2·R·r2) SA = (2π2·R) d/dr r2 SA = ( 2π2·R) 2r1 SA = 4π2·R·r Resources Content, HTML, graphics & design by Bill Willis 2024