Newton's Law of Universal Gravitation Isaac Newton compared the acceleration of the moon in orbit around the Earth to the acceleration of objects as they fall on Earth. Newton proved that the force that causes, for example, an apple to fall toward the ground, is the same force that causes the moon to fall around, or orbit, the Earth. This universal force also acts between the Earth and the Sun, or any other planet and its satellites. Each attracts the other. Believing that gravitational forces were responsible for an apple falling as well as holding the Moon in its orbit, Newton was able to recognize the dependence of gravity upon distance. He concluded that the force of gravity between the Earth and other objects is inversely proportional to the square of the distance separating the Earth's center from the object's center. This means that as the distance between two masses increases, the force will get smaller, as the square of the distance. This is the inverse square law. Newton also realized that the force of gravity depends on the mass experiencing the force, as he described in his second law, Fnet = m·a. He knew as well that the force that attracts one mass to another, and causes, for example, an apple to fall to the ground (towards Earth) must also depend on the size of those masses. Because the force acting to cause the apple's downward acceleration also causes the earth's upward acceleration (Newton's third law), that force must also depend upon the mass of the Earth. His conclusion: The force of gravity acting between the Earth and any other object is directly proportional to the mass of the Earth, directly proportional to the mass of the object, and inversely proportional to the square of the distance that separates the centers of the earth and the object. Newton's genius lay in the fact that he realized gravitation is universal. All objects attract each other with a force of gravitational attraction. Gravity is universal. This force is directly dependent upon the masses of both objects and inversely proportional to the square of the distance that separates their centers. Since the force of gravity is directly proportional to the mass of both interacting objects, more massive objects will attract each other with a greater gravitational force. As the mass of either object increases, the force of gravity between them also increases. Some examples: If the mass of one of the objects is doubled, then the force of gravity between them is doubled. If the mass of one of the objects is tripled, then the force of gravity between them is tripled. If the mass of both of the objects is doubled, then the force of gravity between them is quadrupled. Since the force of gravity is inversely proportional to the square of the distance between the two interacting objects, greater distance will result in a weaker force. So as two objects are separated from each other, the force of gravitational attraction between them also decreases. Some examples: If the separation distance between two objects is doubled (increased by a factor of 2), then the force of gravitational attraction is decreased by a factor of 4 (2 squared). If the separation distance between any two objects is tripled (increased by a factor of 3), then the force of gravitational attraction is decreased by a factor of 9 (3 squared). Using a constant of proportionality G, the relationship can be written as an equation: 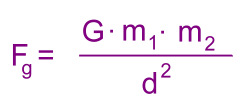The constant of proportionality (G) in the above equation is known as the Universal Gravitation Constant. The units of Fg, the force of gravity, are in Newtons, in his honour. The precise value of G was eventually determined experimentally by Henry Cavendish in the century after Newton's death. The value of G was found to be G = 6.673 x 10-11  N·m2/kg2 Here are a few problems solved using this equation. We're using metric kg/m/s units. Problem 1: "Determine the force of gravity between the Earth and a 70 kg student, if the student is standing at sea level". The necessary information: Mass of Earth: M = 5.98 x 1024 kg    Mass of student: m = 70 kg Radius of Earth: d = 6.38 x 106 m (ignoring the small distance from the surface of the Earth up to the centre of the student, which would be negligible here) Fg = G·M·m            d2 Fg = (6.673 x 10-11)·(5.98 x 1024)·(70)                 (6.38 x 106)2 You can enter this in one step on your Ti calculator; remember to enter the brackets, and enter scientific notation on a Ti correctly. Fg = 686 Newtons Problem 2: "Determine the force of gravitational attraction between the Earth and a 70 kg student, if the student is in an airplane 40,000 feet above the Earth's surface". There are two complications. First, the distance between the two masses is the sum of the Earth's radius and the height above the surface of the student. Second, the latter distance is given in feet, which must be changed to metres. The necessary information: Mass of Earth: M = 5.98 x 1024 kg    Mass of student: m = 70 kg Distance between masses: Radius of Earth: d1 = 6.38 x 106 m Height of student above ground: d2 = 40,000 feet = 12,192 metres (12.19 km) Total distance d = (6.38 x 106) + (1.22 x 104) = 6.39 x 106 m Fg = G·M·m            d2 Fg = (6.673 x 10-11)·(5.98 x 1024)·(70)                 (6.39 x 106)2 Fg = 684 Newtons Now let's compare the two answers to identify an important conclusion: Force of gravity at the surface of Earth is 686 N Force of gravity at a height of 12.19 km is 684 N At 12 km high, the force of gravity has decreased by just a tiny amount. (0.3%) Problem 3: Find the force of gravity on a 70 kg astronaut in the International Space Station 400 km above Earth: Height above surface = 400 km = 400,000 m = 4.00 x 105 m Distance d to centre of Earth = (4.00 x 105) + (6.38 x 106) = 6.78 x 106 m Fg = G·M·m            d2 Fg = (6.673 x 10-11)·(5.98 x 1024)·(70)                 (6.78 x 106)2 Fg = 608 Newtons Again, let's compare this to gravity here on the surface: Force of gravity at the surface of Earth is 686 N Force of gravity at the International Space Station (400 km) is 608 N At 400 km high, the force of gravity has decreased by a small amount (11%) This illustrates the fact that astronauts in orbit are not 'weightless' because there is no gravity; the force of gravity on them is almost as strong as here on the surface. Find out why they are considered weightless. Problem 4: Calculate the force of gravity on a 70 kg astronaut at the distance of the Moon: Distance d between Earth and the Moon is 384,400 km  or 384,400,000 m  or 3.84 x 108 m Fg = G·M·m            d2 Fg = (6.673 x 10-11)·(5.98 x 1024)·(70)                 (3.84 x 108)2 Fg = 189 Newtons Again, let's compare this to gravity on the surface of the Earth: Force of gravity at the surface of Earth is 686 N Force of gravity at the distance of the moon is 189 N At the Moon's distance, the force of gravity is still considerable, although it has decreased by 72% This illustrates two facts: Earth exerts a considerable gravitational force even at the distance of the moon. Using the mass of the Moon instead of the mass of a small astronaut would reveal the much larger gravitational force on the Moon, sufficient to hold it in orbit. Analysis of the numbers would confirm that the gravitational force is decreasing as the square of the distance. Incidentally, the force of gravity continues to decrease with distance, but never actually reaches zero, however far away you are. This is asymptotic behaviour. Now let's look at Newton's three Laws of Motion Newton | Universal Gravitation | Laws of Motion | Calculating Masses | Mass of Jupiter