|
To determine the mass of a planet, it must have a satellite. Scientists need to know two things: how long it takes the satellite (a moon) to orbit the planet (called the period), and how far away the moon is from the centre of the planet. Both of these values have long been measureable; Galileo did it for the moons of Jupiter. Newton's Universal Law of Gravitation can be used to calculate the mass of any astronomical body that has a moon. However, Newton couldn't do it because the magnitude of the constant 'G' in the formula was not known at the time. The value of G was finally experimentally determined by Henry Cavendish in the 18th century to be the extemely small force of 6.67 x 10-11 Newtons between two objects weighing one kilogram each, and separated by one metre. It now became possible to find a formula to calculate a planet's mass! Here's how the formula is derived. Let's start with Newton's Universal Law of Gravitation: 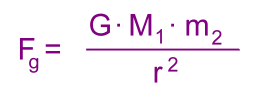
M1 is the mass of the planet m2 is the mass of the moon r is the distance between the planet and moon We'll also use the formula for centripetal force: 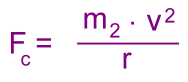 v is the orbital velocity of the moon Finally, we'll need a formula for orbital velocity, based on the fact that the moon's speed, assuming a nearly circular orbit, is the total distance travelled in one orbit divided by the time to complete one orbit (the period). These are 2πr and T. 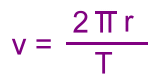
We'll begin by recognizing that the gravitational force Fg holding the moon in orbit about the planet must be equal to the centripital force Fc: 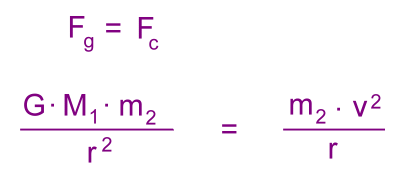 M1 is the mass of the planet m2 is the mass of the moon 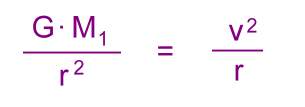
Divide both sides by m2 to eliminate it 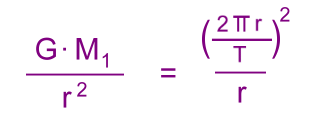
Substitute the orbital velocity formula for v Now we solve for M1, the mass of the planet: 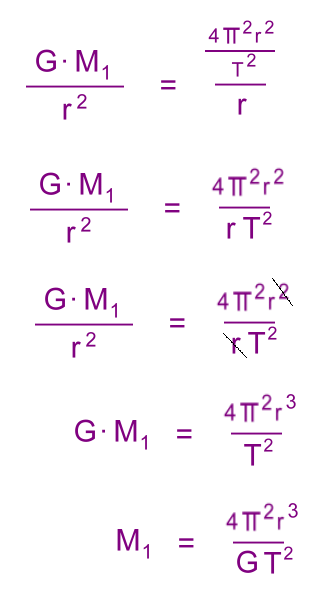
This leaves us with a formula for the mass M1 of a planet with a moon: 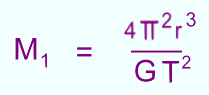 r is the moon's radius of orbit G is the Gravitational Constant T is the period of the moon's orbit Notice a few things: - The similarity to Kepler's Second Law - The fact that we do not need to know the mass of the orbiting moon This is a powerful formula. It can be used, for example, to find such things as the mass of other stars with planetary systems, or the mass of a black hole that has a star orbiting it! Let's use the formula to calculate the mass of Jupiter. |