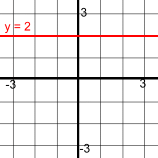
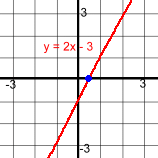
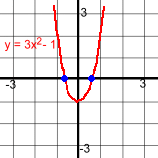
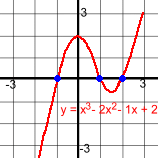
In mathematics, a polynomial is a mathematical expression consisting of variables and coefficients, that involves only the operations of addition, subtraction, multiplication, and positive-integer powers of variables. For example, 3x2 - 5x + 7 is a polynomial, The variable is x. The coefficients are 3, -5, and 7. The word polynomial comes from the Greek poly, meaning "many", and the Latin nomen, or "name". The various types of polynomials can be named two different ways: by the number of terms, and by the degree of the polynomial. Polynomial Names by Number of Terms One Term Polynomials: These polynomials have only one term, so they are called MONOMIALS Examples: 3x2, -4x, 17, ¼x3 Two Term Polynomials: These polynomials have two terms, so they are called BINOMIALS Examples: 4x - 3, 7x2 + 6, 3x5 - 5x2, x + 1 Terms are separated by + or - signs. Three Term Polynomials: These polynomials have three terms, so they are called TRINOMIALS Examples: 3x2 - 5x + 4, x3 + 9x2 - 4, x2 - x + 3 Polynomials with more than three terms don't have special names. For example, 2x3 - 5x2 + 3x - 1 has four terms. It's just called a four term polynomial. Polynomial Names by the Degree The degree of a polynomial is the largest exponent on any of the terms. For example, 3 + x4 - 5x2 has three terms. The highest exponent is 4 So this is a polynomial of degree 4. NOTE: Polynomials are usually written in descending order of powers. So the trinomial above should more properly be written as x4 - 5x2 + 3. This places the highest power first, making it easy to see the degree. But watch out; sometimes they're not in order. Different degrees also have names: Degree 0: Polynomials of degree zero are called CONSTANT polynomials. For example, 2 is a constant. There is no variable, so its value is always 2. These are degree zero because they can be written this way: 2x0 since x0 = 1, so 2x0 = 2(1) = 2. Degree 1: Polynomials of degree one are called LINEAR polynomials. For example, 2x - 3 is degree one and linear. This is because the highest exponent is 1. When the exponent on the variable is 1 or 0, the exponents can be left out: 2x - 3 is really 2x1 - 3x0. Here are some more linear polynomials: 5x, ¾x + 11, 17 - x or 5x1, ¾x1 + 11, 17 - x1 Degree 2: Polynomials of degree two are called QUADRATIC polynomials. For example, 3x2 - 1 is degree two or quadratic because the highest exponent is 2. Here are some more quadratic polynomials: 4x2 + 5x - 3, 1 - 8x2, ⅓x2 Degree 3: Polynomials of degree three are called CUBIC polynomials. For example, x3 - 2x2 - 1x + 2 is degree three or cubic as the highest exponent is 3. Here are some more cubic polynomials: 5x3 + 4x2 - 1, 5 - 7x3, ½x3 + 4x2 - 8x + 9 Similarly, polynomials of degrees 4 and 5 are called QUARTIC and QUINTIC. Correlations: Names by degree correspond to the maximum number of x-intercepts and the shape of the corresponding function:
|