 example 1: a = 1 and it factors x2 - 7x + 12 = 0 (x - 4)(x - 3) = 0 either (x - 4) = 0 » x = 4 or (x - 3) = 0 » x = 3 x = 4 or x = 3 example 2: a ≠ 1 but 'a' is a common factor -2x2 + 20x -50 = 0 -2(x2 - 10x + 25) = 0 -2(x - 5)(x - 5) = 0 either (x - 5) = 0 » x = 5 or (x - 5) = 0 » x = 5 x = 5 example 3: a ≠ 1 and it factors using decomposition 6x2 + 11x - 10 = 0 6x2 + 15x - 4x - 10 = 0 3x(2x + 5) - 2(2x + 5) = 0 (2x + 5)(3x - 2) = 0 either (2x + 5) = 0 » x = -5/2 or (3x - 2) = 0 » x = 2/3 x = -2.5 or x = 0.666... example 4: it doesn't factor In this case, we'll have to use the General Quadratic Formula: To solve ax2 + bx + c = 0, the answers are given by: 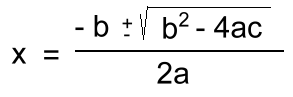
Here are a few examples: example 4a: 2x2 + 5x - 1 = 0 a = 2 b = 5 c = -1 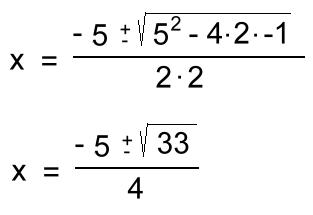 These irrational answers can't be simplified, so can be left as exact answers like this. They could also be evaluated. example 4b: 3x2 - 2x - 4 = 0 a = 3 b = -2 c = -4 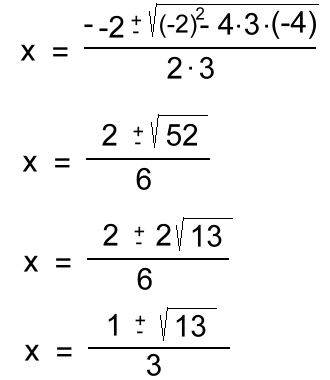 In this example, the final radical has to be simplified, and then all three terms can be reduced. example 4c: 5x2 + 4x + 1 = 0 a = 5 b = 4 c = 1 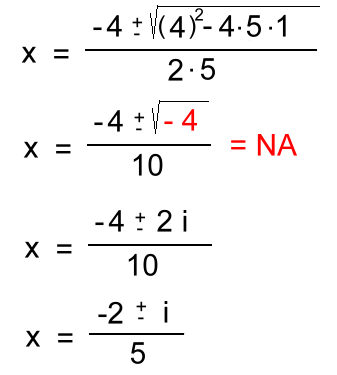 Here the two radical answers are imaginary, so Math10 students can say there is no Real answer. Math 20/30 students will need to simplify it. The General Quadratic Formula can actually be used to solve ANY of the types of quadratic equations. We won't show that. Now let's look at how quadratic equations relate to quadratic functions ... |