 Here is a quadratic function: y = 2x2 + 4x - 6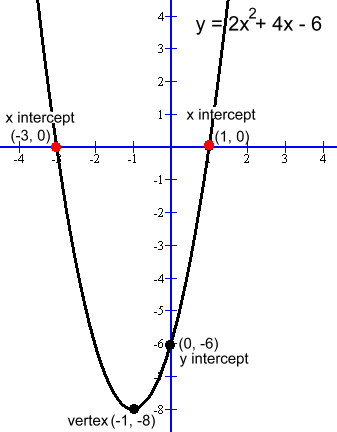 
The function is the set of all points (x, y) that make the equation true.
We could experiment to find points, such as (2, 10). However, we're going to find some key points using algebra, and graph them:The y intercept is a point (0, y) where x is zero: y = 2(0)2 + 4(0) - 6 y = 0 The y intercept is (0, -6) We'll complete the square to find the vertex: y = 2x2 + 4x - 6 y = 2(x2 + 2x + 1) - 2 - 6 y =2(x + 1)2 - 8 Vertex (-1, -8) The x intercepts are the points (x, 0) where y = 0 2x2 + 4x - 6 = 0 Solve this quadratic equation: 2(x2 + 2x - 3) = 0 2(x + 3)(x - 1) = 0 x intercepts (-3, 0) and (1, 0) The solutions to the quadratic equation ax2 + bx + c = 0 are the x intercepts of the quadratic function y = ax2 + bx + c |