 Solving Algebraically ELIMINATION Page Two
Example 4: 7x - 4y = 50 3x - 1 = 17 You may notice that the second equation has no y term. Let's solve it for x: 3x - 1 = 17 3x = 18 x = 6 This is a vertical line. For our purposes, algebraically, we now know one coefficient of the solution. Substitute in the other equation to find the other value: 7x - 4y = 50 7(6) - 4y = 50 -4y = 8 y = -2 solution is (6, -2) Example 5: 0.4x + 0.3y = 1.9 0.2x + 0.5y = 2.7 While we could solve with the decimals left in, let's remove them first: multiply all terms by 10 4x + 3y = 19 2x +5y = 27 Now double the second equation: 4x + 3y = 19 4x +10y = 54 This makes the x terms the same size 0x - 7y = -35 so we can subtract term by term: y = 5 0.4x + 0.3y = 1.9 Substitute in one of the original equations: 0.4x + 0.3(5) = 1.9 0.4x + 1.5 = 1.9 0.4x = 0.4 x = 1 solution (1, 5) Example 6: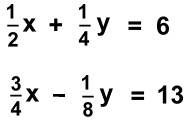 
In this example we're going to remove the fractions first.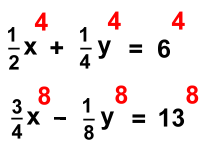 
Multiply the first equation by 4 and the second by 8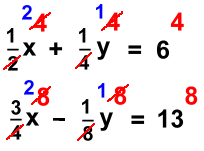 
Reduce. All the denominators will disappear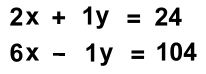 
No need to multiply; the y coordinates are already the same Add the equations to eliminate the y's 2x + 1y = 24 6x - 1y = 104 8x = 128 x = 16 We'll substitute this to find y. We have to use an original equation. We'll choose the first equation: 1/2x + 1/4y = 6 1/2(16) + 1/4y = 6 8 + 1/4y = 6 1/4y = -2 y = -2÷(1/4) = -2(4) = -8 solution is (16, -8) We chose to stick with fractions rather than changing to decimals; we didn't have to, as none of the fractions resulted in repeating decimals, which would have necessitated rounding. Rounding will make your answers approximate, which may not be desired. Example 7: 2x + 5y = 12 6x + 15y = 20 Since the x and y terms in the second equation are a multiple of the first equation, this system has no solution, as the lines are parallel. Example 8: Finally, an example of a real problem that illustrates how elimination can be used to solve it. "Mary's order of three bottles of shampoo and five bottles of conditioner cost $51. Edith's order of seven bottles of shampoo and one bottle of conditioner cost $39. What is the price of one bottle of each?" [Yes, this is a silly problem that no-one would ever do math to solve. It's an analogy. Math textbooks and teachers often use analogies, for a very good reason. Find out why here]. We're going to change a problem in words into a math problem with equations, because we know we can solve that. Let 'x' be the cost of one bottle of shampoo, and 'y' the cost of one bottle of conditioner. Make the equations: 3x + 5y = 51 7x + y = 39 Multiply the second equation by 5: 3x + 5y = 51 35x + 5y = 195 and subtract the equations to eliminate the y's: -32x = -144 x = 4.5 Substitute this in the second equation: 7(4.5) + y = 39 31.5 + y = 39 y = 7.5 The solution to the word problem is: A bottle of shampoo costs $4.50 and a bottle of conditioner costs $7.50 Important: The check for a word problem is done by seeing if the answers work in the problem: Three bottles of shampoo and five bottles of conditioner 3($4.50) + 5($7.50) = 13.50 + 37.50 = $51 checks Seven bottles of shampoo and one bottle of conditioner 7($4.50) + $7.50 = 31.50 + 7.50 = $30 checks Checking in the words of the problem makes sure that you didn't mistranslate and make incorrect equations. If you'd done that, and merely checked in the equations, the check might have worked, leading you to believe the answer was correct. |