 Solving Graphically We'll look at the following system of lines: The solution will be the point where the two lines intersect. 2x - 4y = 8 3x + 4y = 12 We'll graph the first equation by solving it for Y and making a table of points: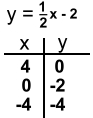 
2x - 4y = 8-4y = -2x + 8 y = 2/4x - 2 y = ½x - 2 Now we can plot the points [You can use a graphing calculator to generate the points, and check your answers] We'll graph the second equation by finding its intercepts: 3x + 4y = 12 x intercept: y=0 3x + 4(0) = 12 3x = 12 x = 4 x intercept (4, 0) y intercept: x=0 3(0) + 4y = 12 4y = 12 y = 3 y intercept (0, 3) Here is the gaph with both lines plotted, and the solution identified: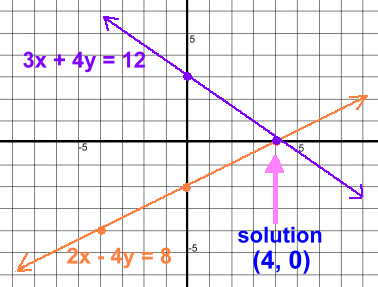 
In this particular example, the solution (4, 0) appeared in both sets of generated points before we even graphed the result, so we know it's the exact answer. If that hadn't happened, or if the solution was between grid lines and had to be estimated, we would have to substitute it into the two equations to see if it worked, as reading values from a graph can be inaccurate. The solution would also need to be rounded. Let's look at a second example: y = 3x - 4 y = 3x + 6 From what you know about parallel lines, you can tell that both these lines have slope 3, so they're parallel. This means there is no solution. A third example: 6x - 2y - 4 = 0 y = 3x - 2 Let's solve the first one for Y so both can be graphed: 6x - 2y - 4 = 0 -2y = -6x + 4 y = 3x - 2 Here we discover that this first line is identical to the second; the fact that it had been rearranged to standard form hid that from us. Both are the same line; if we graph them we'll get lines graphed in the same spot, with an infinite number of intersection points. With no single unique intersection point, we say that there is no solution. Now let's move on to algebraic solutions >>> |