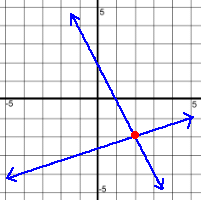
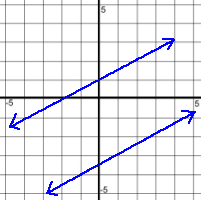
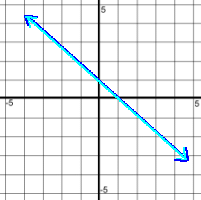
You've learned about lines in a previous math course, including how to graph them in various ways, how to find their Y intercepts, how to make their equations, and how to solve for Y.

Now let's look at how to solve a system of linear equations.

A system of equations is a set of two or more equations for which the solution is the single point or points on a graph where they intersect. On these pages we'll be looking at systems with just two equations, both of which will be lines.

Here's what can happen when two lines are graphed together:


Consistent System
Just one intersection point.
The solution is the point.
  

Inconsistent System
No intersection point; the lines are parallel. No solution. 		 

Inconsistent System
Infinite intersections; the two lines are the same. No solution.


Here are the ways you can find the solution (if one exists) to a system of lines:
  • Graphically Use any method to graph the two lines to find the intersection point
  • Algebraically Use one of three algebraic methods to solve for the solution without graphing:
    • Substitution
    • Comparison
    • Elimination
Graphing may not be accurate, and takes more time. Algebraic methods are often quicker and always give an exact answer.

NOTE: On these pages we will see some linear equations in Standard Form, which we reserve for equations of the form Ax + By + C = 0. This aligns with the definition used in Math 30 for other types of equations. Your textbook for linear systems may label equations of the form Ax + By = C as 'Standard Form'; we don't. See more about equation forms here.

We'll also be using the principle that says that when you multiply all the terms in an equation by the same constant, the new equation is completely equivalent to the original; it's the same line.
ie: 4x + 3y = 12  and  40x + 30y = 120  are equivalent.

Other methods for solving linear systems include using the 'intersect' menu item on a a graphing calculator, or using a formula for the solution points. We won't look at these, although the former is a skill needed for Math 20 and 30

Let's start by looking at the graphing method >>>


Introduction | Solving Graphically | Solving Algebraically | Mixed Practice



Resources


Content, HTML, graphics & design by Bill Willis 2024