
This page will explain how to obtain and use the standard form of the equation of the conic section called a circle, to produce a graph. It will also show you how to convert between the standard and general form of the circle equation. There is also a quiz.
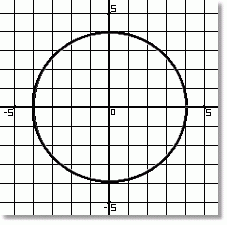
On the right is a simple circle centred at (0, 0). Its radius is 4.
The equation of any circle centred at (0, 0) looks like this:
x2 + y2 = r2
where r is the radius.
The equation of the circle at the right is then:
x2 + y2 = 16
Every circle centred at the origin will have this sort of equation.
|
|
For example, the equation x2 + y2 = 25 would be a circle centred at the origin with radius 5
Circles with centres off the origin show horizontal and/or vertical translations in their equations. Since the values for the translation(s) are with their respective variables, the shifts are opposite to the direction indicated in the equation.
Here's an example to show you what we mean:
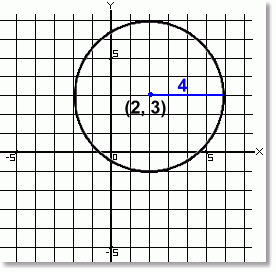
The circle at the right is centred at (2, 3).
Its radius is 4.
The equation of this circle is:
(x - 2)2 + (y - 3)2 = 42
or:
(x - 2)2 + (y - 3)2 = 16
Notice that both the horizontal (right 2) and vertical (up 3) translations are shown in the equation with a sign opposite to their directions.
|
|
Here's another example:
|
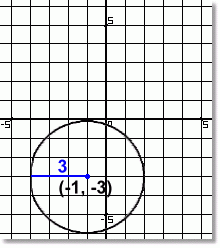
This circle has a centre at (-1, -3).
Its radius is 3.
The equation of this circle is:
(x + 1)2 + (y + 3)2 = 32
or:
(x + 1)2 + (y + 3)2 = 9
Again notice that the translation direction is opposite to what the equation shows. This will always be the case when the shift is with the variable.
|
What happens when the circle equation is not in standard form?
For example, suppose we take the circle equation above and simplify it:
(x + 1)2 + (y + 3)2 = 9
x2 + 2x + 1 + y2 + 6y + 9 = 9
x2 + y2 + 2x + 6y + 10 = 9
x2 + y2 + 2x + 6y + 1 = 0
|
This last line, where all terms have been simplified and the equation has been rearranged so that it equals zero, is called the general form of the equation. Notice that in this version, neither the centre (-1, -3) or the radius 3 is evident.
The general form of the equation is does give you some information, however:
x2 + y2 + 2x + 6y + 1 = 0
The fact that the coefficients in front of the x2 and y2 terms are equal (and both the same sign) tells you it is a circle equation.
If they were different numbers, the equation would be an ellipse. If they were opposite signs, the equation would be a hyperbola. If one of them were missing, it would be a parabola.
Now we need to be able to take a circle equation in general form and rewrite it so that it is in standard form, so that we can graph it. This operation is called 'completing the squares'.
Let's start with a brand new equation, in general form:
x2 + y2 + 8x - 2y + 13 = 0
x2 + 8x + y2 - 2y = - 13
x2 + 8x + ___ + y2 - 2y + ___ = -13
x2 + 8x + 16 + y2 - 2y + 1 = -13 + 16 + 1
(x + 4)2 + (y - 1)2 = 4
|
The first step is to reaarange the equation, placing the 'x' terms first, then the 'y' terms, and moving the constant term (13) to the other side.
Next we're going to make a perfect square from the 'x' terms and the 'y' terms. The blanks are for the third term in each trinomial we will make.
The numbers we add are 'half of each second coefficient, squared'. In this case, half of 8 squared and half of -2 squared, or 16 and 1.
These numbers must be added to the right side as well to preserve the equality.
|
Finally, factoring each perfect square trinomial on the left, and simplifying the right, yields the standard form of the equation.
This circle has centre (-4, +1) and radius 2
Try a QUIZ about locating circles in standard form.
You can also visit our pages about ellipses, hyperbolas and parabolas
Resources
Content, HTML, graphics & design by Bill Willis 2023
|


