 
This page provides a brief introduction to orbital mechanics, specifically the orbits of spacecraft and satellites as described by grade 12 mathematics. 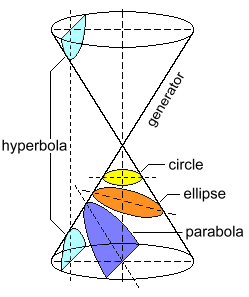 A conic section, or just conic, is a curve formed by passing a plane through a right circular cone. As shown at the right, the angle of the plane relative to the cone determines whether the conic section is a circle, ellipse, parabola, or hyperbola. You can visualize the four conic sections by cutting modelling clay. The circle and ellipse arise when the intersection of cone and plane is a closed curve. (The circle is a special case of the ellipse where the plane is perpendicular to the axis of the cone). If the plane is parallel to one of the generator lines of the cone, the conic is called a parabola. Finally, if the intersection with the plane is not parallel to a generator line of the cone, the figure is a hyperbola. In the latter case the plane will intersect both halves of the cone, producing two separate curves. 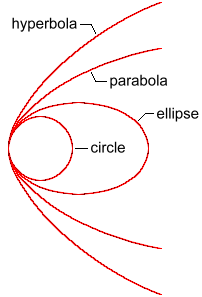
All conic sections can be described in terms of their eccentricity. Eccentricity measures how stretched out the orbit or curve is; it can be calculated by dividing the distance between the foci by the length of the major axis, and is a number between zero and one. An eccentricity of zero indicates a circle. The type of conic section is also related to the semi-major axis and the energy of the corresponding orbit. The table below shows the relationships between eccentricity, semi-major axis, and energy and the type of conic section. Satellite orbits can be any of the four conic sections. This page deals mostly with elliptical orbits, though we will also look briefly at hyperbolic orbits.  An orbiting satellite follows an oval shaped path known as an ellipse, with the body being orbited, called the primary, located at one of two points called foci. An ellipse is defined to be a curve with the following property: for each point on an ellipse, the sum of its distances from two fixed points, called foci, is constant. The longest and shortest lines that can be drawn through the center of an ellipse are called the major axis and minor axis, respectively. The semi-major axis is one-half of the major axis and represents a satellite's mean distance from its primary. For example, the Earth orbits the sun in a path that is an ellipse, but one with an eccentricity of only 0.0167. Since this value is close to zero, the center of Earth's orbit is relatively close to the center of the Sun, relative to the size of the orbit. Stated another way, Earth's orbit is very close to being a circle. The seasons on Earth are therefore NOT related to how far the Earth is from the sun. Rather, they are due to the inclination of the Earth's axis relative to its orbit, about 23 degrees, which, for example, causes the northern hemisphere to point directly at the sun in summer. Inclination (which is not discussed in high school math) is the angle between a satellite's orbital plane and the equator of its primary. By definition, the Earth's orbit around the sun, for example, is at an angle of 0 degrees; all other planetary bodies' orbits are in reference to this. Types of Orbits For a spacecraft to achieve Earth orbit, it must be launched above the Earth's atmosphere and accelerated to orbital velocity. The most energy efficient orbit, one that requires the least amount of propellant, is one that is launched from as close to the equator as possible. To achieve this, a spacecraft is launched in an eastward direction to take advantage of the rotational speed of the Earth. At the United States' launch site in Cape Canaveral, for example, (28.5 degrees north latitude) a due east launch results in a velocity boost of 1,471 km/h. Launching a spacecraft in a direction other than east, or farther from the equator, results in an orbit of higher inclination. High inclination orbits are less able to take advantage of the initial speed provided by the Earth's rotation, so the launch vehicle must provide a greater part of the energy required to attain orbital velocity. The advantages over equatorial orbits include satellites being able to pass directly over higher latitudes. Below we describe several types of orbits and the advantages of each. The rules of orbital mechanics are sometimes counter-intuitive. If you increase the velocity of a spacecraft in the direction it's orbiting, it will move outwards into a larger orbit, where it slows down. Alternately, if the spacecraft is made to slow down, it will drop down to a lower orbit, where it speeds up! If two spacecraft are in the same circular orbit and wish to dock, unless they are very close, the trailing craft cannot simply fire its engines to go faster. This will change the shape of its orbit, causing it to gain altitude and actually slow down relative to the leading craft, missing the target. The space rendezvous before docking normally takes multiple precisely calculated engine firings in multiple orbital periods, requiring hours or even days to complete. To send a spacecraft to an inner planet, such as Venus, the spacecraft must be launched and accelerated in the direction opposite of Earth's revolution around the sun (i.e. decelerated) until it achieves a sun orbit with a perihelion equal to the orbit of the inner planet. To reach any planet, the spacecraft be inserted into an interplanetary trajectory at the correct time so that the spacecraft arrives at the planet's orbit when the planet will be there! This task is comparable to a quarterback "leading" his receiver so that the football and receiver arrive at the same point at the same time. The interval of time in which a spacecraft must be launched in order to complete its mission is called a launch window. The Hyperbolic Orbit So far we've been looking at elliptical orbits, where a spacecraft has insufficient velocity to escape the gravity of its primary. Satellites in elliptical low Earth orbits achieve speeds of 27,000 km/h, or about 7.5 kilometres per second. There is a velocity, called the escape velocity, Vesc, such that if the spacecraft is launched with an initial velocity greater than Vesc, it will travel away from the planet and never return. To achieve escape velocity we must give the spacecraft enough kinetic energy to overcome all of the gravitational potential energy. A space vehicle that has exceeded the escape velocity of a planet will travel a hyperbolic path. Earth's escape velocity is about 11 kilometres per second or 40,000 km/h. The velocity of escape from the less massive Moon is about 2.4 kilometres per second at its surface. The formula for calculating the escape velocity from any celestial body is: 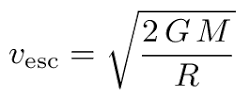 where G is the universal gravitational constant 6.67408 x 10-11 M is the mass of the body R is the radius of the body A planet or moon cannot long retain an atmosphere if its escape velocity is low enough to be near the average velocity of the gas molecules making up the atmosphere. Inside the event horizon of a black hole, the escape velocity exceeds the speed of light, so not even rays of light can escape into space. |