The Ellipse ........................................

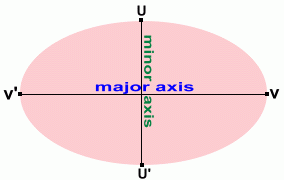
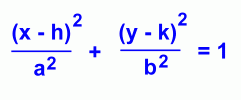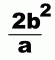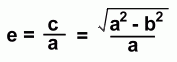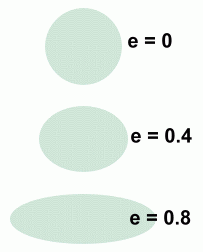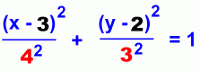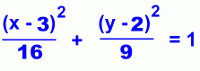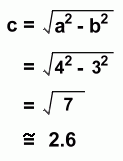An ellipse is a conic section, like parabolas, hyperbolas and circles, that is a stretched circle. It is longer than it is wide. In our example here, it is longer in the horizontal direction. This length is called the major axis, and the ends are the vertices. The up-and-down width is called the minor axis.

This page will provide you with many facts and formulas that relate to ellipses. This topic is no longer in the Math 30 curriculum, but will be important in college engineering, math or physics courses.

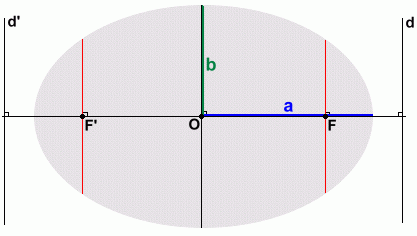
The semi-major axis from the centre O to vertex V has distance a
The semi-minor axis from centre O to the top has distance b

Two additional features of an ellipse are the focus and the directrix. There are two of each:

- the two focuses (foci) are on the major axis, and are marked F and F'. They are inside the ellipse.
- the two directrixes are lines d and d', perpendicular to the major axis They are outside the ellipse.

The latus rectum is the distance across the ellipse at the focal point. There is one at each focus. They are shown in red.
The length of a latus rectum is given by this formula:

A visitor to our site wondered where this formula came from, so we worked out the derivation for those who are interested.

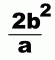
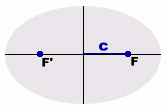
The distance to the focus from centre O is labelled c

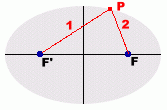
The focal points are used to generate the ellipse. If you find all the points P where distances 1 and 2 always add to the same amount, the points P will form an ellipse.
You can do this with a piece of string, two tacks, and a pencil. See an animated illustration of this fact here .

This sum of the distances from any point P on the ellipse to the two foci is equal to the length of the major axis, 2a.

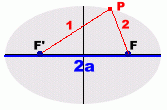
distance 1 + distance 2 = 2a

Here are the mathematical relationships between these measurements:

a is the biggest of the three values, and they're related this way:

The focal distance c can be calculated by solving the formula for c:

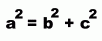
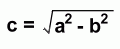
The eccentricity of an ellipse is a measure of how elongated it is.

Circles have an eccentricity of 0

The more stretched out an ellipse is, the larger the value of the eccentricity ... until the ellipse 'breaks' and becomes a parabola, with eccentricity 1.

The eccentricity of an ellipse is always a value between 0 and 1. The larger the value, the more elongated the ellipse.

e is the symbol for eccentricity. It can be calculated using this relation:

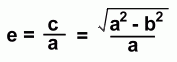
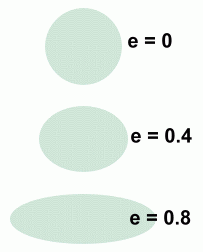
There is also a relation between the eccentricity and the distance to the directrix:

You can find the area of an ellipse using this formula:

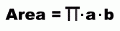
On a Cartesian plane, an ellipse has an equation based on the values of a and b. The value a, which is the length of the semi-major axis, is associated with the horizontal axis if the ellipse is horizontal, and the vertical axis if the ellipse is vertical.
For our example, the ellipse is horizontal, so a² goes under the x² and b² goes under the y².
This would reverse if the ellipse were vertical.

Let's look at a real example ...

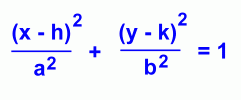
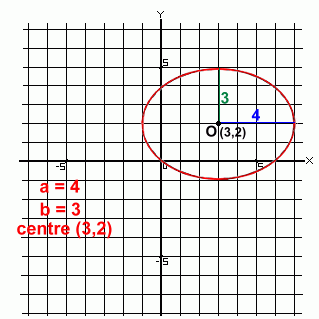
Let's look at a horizontally stretched ellipse that is 8 units wide and 6 units high, and shifted so that its centre is at the point (3,2).

First, notice that the rule for translating an image is followed; the centre (3,2) is equivalent to a shift right 3 and up 2, and is apparent in the equation:

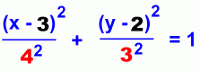
where a = 4 and b = 3.
This simplifies to:

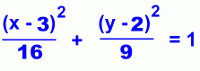The value of a² is under the x² term because the ellipse is horizontal. If it were vertical, the 16 and 9 would be reversed.

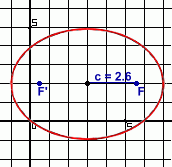
The location of the foci can be determined by calculating the value of c:

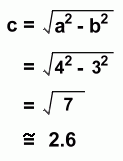
Notice that the focal distance is about 2.6 units from the centre of the ellipse. That would make the focal points F (5.6, 2) and F' (0.4, 2)

Resources