X and Y Intercepts

The intercepts of a line are the points where the line crosses the x and y axes .


Here is a line that crosses both axes.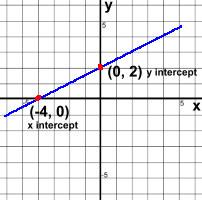

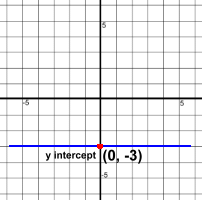
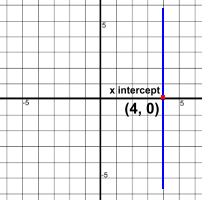
It crosses the x axis at the point (-4, 0).
(-4, 0) is the x intercept of this line.

It crosses the y axis at the point (0, 2).
(0, 2) is the y intercept of the line.

x intercepts always look like this: (X, 0). The y coordinate is 0.
y intercepts always look like this: (0, Y). The x coordinate is 0.


Lines don't always have two intercepts, but they must have one. Remember that lines extend to infinity in both directions, even though we're only showing segments of them here.


This is a horizontal line with
slope 0. It has a y intercept.
  

This is a vertical line with no
slope. It has an x intercept.

Now let's look at how to find the intercepts if you know the rule or equation that generated the points.
In order to do this, you need to remember that:
X intercepts are points with the y coordinate 0
Y intercepts are points with the x coordinate 0

Here's our first example: 4x - 5y = 10

Finding the x intercept: let the y value be 0

4x - 5(0) = 10   and solve for x

4x = 10

x = 2.5

Since y = 0, the x intercept is (2.5, 0) 		  Finding the y intercept: let the x value be 0

4(0) - 5y = 10   and solve for y

-5y = 10

y = -2

Since x = 0, the y intercept is (0, -2)

Knowing that the x intercept is (2.5, 0) and the y intercept is (0, -2), we could plot these points to make a complete graph. We'll come back to this later.



Here's a second example: y = 2x - 4

Finding the x intercept: let the y value be 0

0 = 2x - 4   and solve for x

4 = 2x

2 = x

Since y = 0, the x intercept is (2, 0) 		  Finding the y intercept: let the x value be 0

y = 2(0) - 4   and solve for y

y = -4

Since x = 0, the y intercept is (0, -4)




A third example: 4x + 15 = 0

Let's solve this for x first:

4x = -15

x = -3.75

We have an x coordinate. This must be the x intercept (-3.75, 0)

Since there is no y in the equation, we can't find a y intercept because there isn't one.

This must be a vertical line that crosses the x axis at (-3.75, 0)



A final example: 2y - 8 = 0

Let's solve this for x first:

2y = 8

y = 4

We have a y coordinate. This must be the y intercept (0, 4)

Since there is no x in the equation, we can't find an x intercept because there isn't one.

This must be a horizontal line that crosses the y axis at (0, 4)


Next we're going to explore how to quickly make a graph for some line equations.


Introduction | Slope | Special Lines | XY Axes | Intercepts | Quick Graphing
Linear Equations | Parallel and Perpendicular | Equation Forms | Finding Equations



Resources


Content, HTML, graphics & design by Bill Willis 2023