|
The slope of a line is a measure of how steep it is. There are a number of ways of measuring the steepness of a line. For example, highway steepness, or 'grade', is measured as a percent. In trigonometry, steepness is the tangent of the angle of inclination of the road. We'll use the more general method to measure steepness, which is 'rise divided by run'. This method lends itself nicely to an algebraic approach, which will be necessary later. We'll use the symbol m for slope. Here is a line that, left to right, is moving upward. It passes through points A and B. If you count squares, you can see that, from A to B, you move horizontally a distance of 8, and then rise vertically a distance of 6. 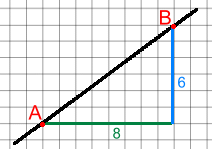 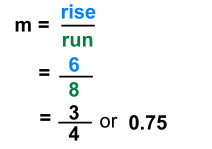 If you think about it: Now let's look at what happens when a line slants downwards. Here is a line that, left to right, is moving downward. It passes through points A and B. If you count squares, you can see that, from A to B, you first drop vertically a distance of - 6, and then travel a distance of 8 horizontally. 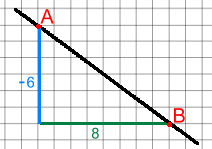 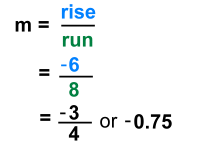 If you think about it: Linear Equations | Parallel and Perpendicular | Equation Forms | Finding Equations |