|
Whether lines are parallel or perpendicular can be determined by looking at the equation of each line, if it's in 'y=' form. The slope of each line determines whether they'll be parallel or perpendicular/ Parallel Lines 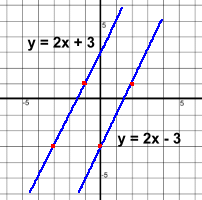 Parallel lines have the same steepness.
They have the same slope.m = 2 for both lines in this example. Here are some more examples of parallel lines: y = -3x + 4 and y = -3x - 8 both have slope -3 y = x + 2 and y = x + 7 both have slope 1 (in front of x) Notice that the y intercepts are different in each case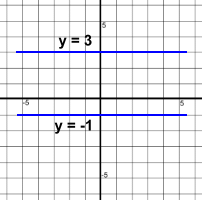 
Horizontal lines all have slope 0 The equations could be written y = 0x + 3 and y = 0x -1 Horizontal lines are always parallel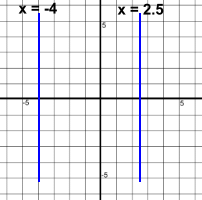 
Vertical lines are also parallel They have no slope, so the rule doesn't work You'll just have to remember that vertical lines are always parallel Perpendicular Lines 'Perpendicular' means 'cross at a ninety degree angle'. What do the equations of two perpendicular lines look like?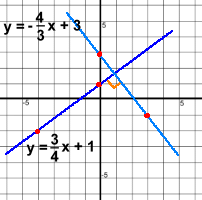 
Once again, only the slopes matter. Look at the slopes of the two lines.One has slope -4/3. The other has slope +3/4 These are negative reciprocals of each other (opposite signs and flipped) Also they multiply to -1 Lines with negative reciprocal slopes will be perpendicular The form of the equation must be 'y ='. The y intercepts are irrelevant Here are some more examples of negative reciprocal slopes: 5/2 and -2/5 3 and -1/3 1/4 and -4 1 and -1 So for example y = 1/4x + 3 and y = -4x would be perpendicular lines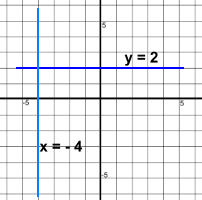 
Horizontal and vertical lines are perpendicular The rule doesn't work because vertical lines have no slope You'll just have to remember that Horizontal and vertical lines are perpendicular Linear Equations | Parallel and Perpendicular | Equation Forms | Finding Equations |