 A satellite in orbit around a central mass usually follows an elliptical path. Common exmples include man-made satellites orbiting Earth, the Moon orbiting Earth, the Earth orbiting the Sun, and the many moons orbiting Jupiter. Often these orbit are nearly circular. Earth's orbit is not a perfect circle; it's elliptical. This means there is one point in the orbit where Earth is closest to the Sun, and another where Earth is farthest from the Sun. This might seem to be the reason for our seasons, but it's not. Winter in the northen hemisphere, for example, occurs when Earth is closest to the Sun. You can find out what actually causes the seasons here. The difference between the Earth's elliptical orbit and a perfect circle, however, is just 3.3%. Seen from above the solar system, or plotting the orbit on paper, you would not be able to tell by eye that the orbit was not circular.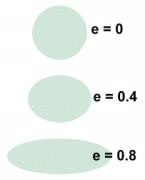 
How elongated an elliptical orbit is can be measured by its eccentricity. Circles have no elongation, so their eccentricity is zero. Comets, on the other hand, spend most of their time far from the Sun, coming closer every once in a while, as explained by Kepler's 2nd Law. They have highly elliptical orbits. Halley's Comet, for example, which comes close to the Sun every 85 years, has an eccentricity of 0.967 Let's look at orbits and describe some of the parameters. We'll look at a circular orbit first.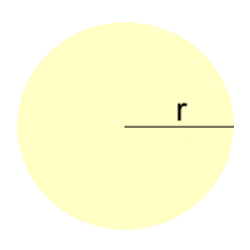 
A circle has just one parameter, its radius r. The radius of a circular orbit is a measure of how far the satellite is from the central body.For example, the orbit of the Moon around Earth is a nearly circular ellipse with an approximate radius of 384,400 km. We can work out the ORBITAL SPEED of the Moon as it circles the Earth. To do this, we'll need to divide the distance it travels during one orbit by the time it takes. The distance around a circle is its circumference, given by the formula C = 2πr. The circumference of the Moon's orbit works out to be 2.42 x 106 km. The time for the Moon to complete one orbit is 27.3 days, or 655.2 hours, or 6.55 x 102 h. This is the PERIOD of the orbit. The Moon's speed can now be calculated by dividing the distance travelled by the time: v = d÷t = (2.42 x 106) ÷ (6.55 x 102) = 3.69 x 103 km/h. We can calculate the Moon's orbital speed another way, using a formula that comes from Newton's laws of gravity: 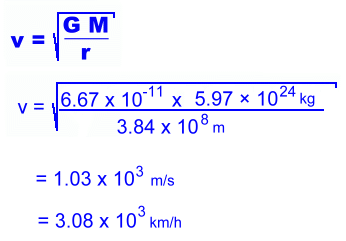 This is in pretty close agreement with our previous calculation, considering all of the approximations we made, including an average value for the Moon's radius of (nearly circular) orbit.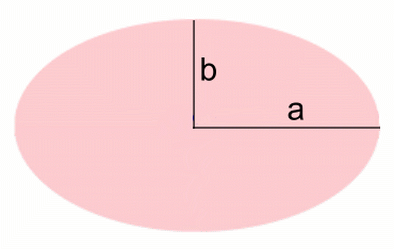 
When the orbit of a satellite is clearly an ellipse with an eccentricity not close to zero, we'll have to use a different method to calculate orbital speed. We could just average the two radii a and b, and use that average for the 'average orbital radius', pretending the orbit is a circle, to work out an 'average orbital speed'. That's what's often done in high school physics textbooks. Let's see if we can be more accurate than that. The difficulty lies in the fact that there is no simple formula for the circumference of an ellipse. The famous Indian mathematician Ramanujan came up with several approximations; we'll use this one for the perimeter of an ellipse:  
The planet Mercury, with an orbital eccentricity of 0.2056, is the planet with the most elliptical orbit in our solar system. Here's the data we'll need for Mercury: a = 5.79 x 107 km b = 5.67 x 107 km period T = 88.0 days = 2.11 x 103 hours 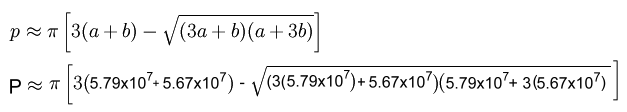 This can be entered in one step on your calculator  Now let's calculate the average speed of Mercury in its orbit: v = d ÷ T = (3.58 x 108 km) ÷ (2.11 x 103 hours) = 1.70 x 105 km/h This matches the average speed of Mercury as given in the astronomical tables. It has to be an average not just because the formula is an approximation, but because, as described by Kepler's Second Law, a satellite like Mercury in elliptical orbit moves at different speeds at various positions in the orbit, faster when closer to the Sun, and slower when farther away. Finally, let's look at Earth satellites in geosynchronous orbits. A geosynchronous orbit about Earth has a period of 23 hours 56 minutes 4 seconds, and is 35,786 km above the Earth's equator. A spacecraft in geosynchronous orbit appears to remain above Earth at a constant longitude. 
To achieve a geostationary orbit, an orbit is chosen with an eccentricity of zero. This orbit is ideal for certain kinds of communication satellites and meteorological satellites. (The idea of a geosynchronous orbit for communications spacecraft was first popularised by science fiction author Sir Arthur C. Clarke in 1945, so it is sometimes called the Clarke orbit).The radius of orbit (from Earth's centre) is Earth's equatorial radius (6378 km) plus satellite height (35,786 km) = 42,164 km Circumference of orbit = 2πr = 2π(42,164) = 264,924 km The period of the orbit is 23 hours 56 minutes 4 seconds or 23.93 hours The satellite's speed will be 264,924 ÷ 23.93 = 11,071 km/h or 3.08 kilometres per second Contrast this with the Space Shuttle's low Earth orbit speed of 27,400 km/h or 7.6 km/s at a height of 200 km. This matches what Kepler said about orbits; the farther the satellite is from the central body, the slower it moves in orbit. |