 
Johannes Kepler was born in 1571 in Germany. He was a Renaissance astronomer, and is best known for discovering three major laws of planetary motion:
Kepler himself did not call these discoveries 'laws', as would become customary after Isaac Newton derived them from a quite different set of general physical principles. Kepler's discoveries gave Nicolaus Copernicus's new Sun-centred system a foundation, with the Sun actively pushing the planets around in noncircular orbits. Kepler's ideas about physical astronomy laid the foundation for Newton's work. Kepler had obtained copy of Copernicus's 1543 book, 'De revolutionibus orbium coelestium libri vi' ("Six Books Concerning the Revolutions of the Heavenly Orbs"). Kepler quickly grasped the main ideas in Copernicus's work, and would make it his mission to demonstrate rigourously what Copernicus had only guessed to be the case. Like many philosophers of his era, Kepler had once held the mystical belief that the circle was the universe's 'perfect shape', and that the planets' orbits must be circular. However, Kepler had inherited a critical resource: Tycho Brahe's detailed observations of the movements of planets in the night sky, particularly those of Mars. In his lifetime Tycho had been stingy in sharing his observations. After his death, Kepler was ultimately able to work with Tycho's very accurate planetary orbit data. For many years, he struggled to make Tycho's observations of the motions of Mars match up with a circular orbit. Eventually he gave up on this idea, realizing that orbits had to be ellipses. With Tycho's data having the precision necessary to back up his hypothesis, Kepler was able to discover his 'first law', that Mars moves in an elliptical orbit. After Galileo built a telescope in 1609 and announced previously unknown objects in the heavens - moons revolving around Jupiter - he sent Kepler his treatise. Kepler responded by sending Galileo copies of some of his own works. These provided strong support for Galileo's discoveries, and Galileo wrote to him, "I thank you because you were the first one, and practically the only one, to have complete faith in my assertions." Kepler eventually published the first textbook of Copernican astronomy, which began with the elements of astronomy and then gathered together all the arguments for Copernicus's theory of the Sun-centred solar system, and added to them Kepler's own new rules of planetary motion. This work would prove to be the most important theoretical resource for the Copernicans in the 17th century. Galileo and Descartes were probably influenced by it. Eventually Isaac Newton would take over Kepler's laws and incorporate them into his own work. Kepler's Laws Explained Kepler's First Law Kepler's first law explains that planets are orbiting the Sun in a path described as an ellipse. An ellipse has two foci, and the Sun must be at one of them. 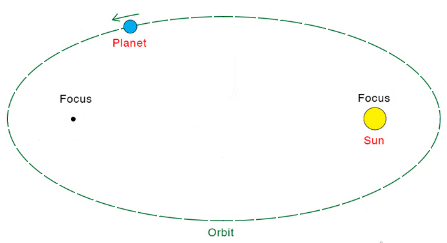 This was not obvious to the observers at the time, because the orbits of the observable planets and moons, and Earth, had elliptical orbits which were nearly circular. Kepler needed the detailed observations of the movement of Mars made by Tycho to show that its orbit must be an ellipse. Kepler's Second Law Kepler's second law, sometimes referred to as the law of equal areas, describes the speed at which any given planet will move while orbiting the Sun. The speed at which any planet moves through space is constantly changing. A planet moves fastest when it is closest to the sun A planet moves slowest when it is furthest from the Sun. This discovery laid the foundations for the science of orbital mechanics. 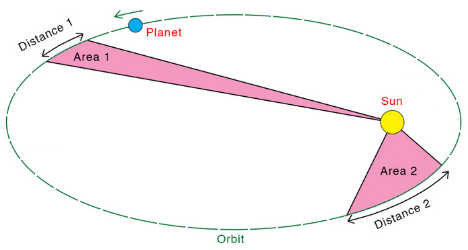 Speed at distance 1 is slower Speed at distance 2 is faster Time taken to travel distance 1 = time taken to travel distance 2 Area 1 = Area 2 Kepler's Third Law Kepler's third law gives a mathematical relationship between the periods and orbital radii for any two bodies that orbit around a central mass. This could be two satellites orbiting the earth, two planets orbiting the Sun, or two moons orbiting a distant planet. The Period T is the time to complete one orbit. The radius of orbit r is the mean distance to the central mass. Here is the relationship, for bodies a and b orbiting a central mass: 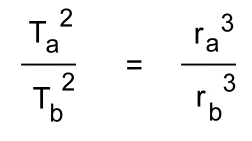 The periods Ta and Tb must have the same units, as must the orbital radii ra and rb. [Astronomical measurements often use Scientific Notation] Knowing any three of these values will let you work out the fourth. Let's look at an example involving two planets, Earth and Pluto, orbiting the Sun. [We're ignoring the fact that Pluto is no longer considered a planet] "Earth has an orbital period of 365 days and its mean distance from the Sun is 1.495 x 108 km. The planet Pluto's mean distance from the Sun is 5.896 x 109 km. Calculate Pluto's orbital period" 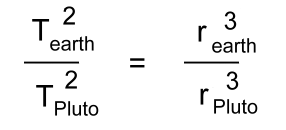 Tearth = 365 days rearth = 1.495 x 108 km Tpluto = ? rpluto = 5.896 x 109 km [Because Earth's period is given in Earth days, the answer for Pluto's period will also be in Earth days] Fill in the three values we know: 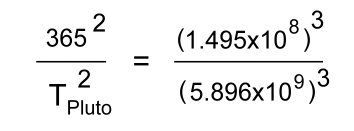 Work out the right side: 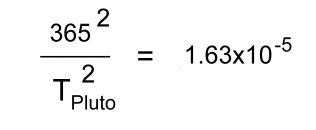 Solve: 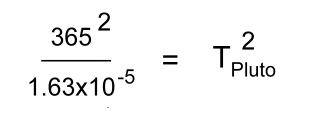 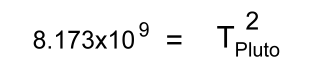 Take the square root of both sides:  This relationship can be used on any orbiting bodies, even planets orbiting a distant star. Kepler's third law was discovered on the basis of comparison of periods and distances of the planets in our own solar system. In 1621 Kepler noticed that Galilean moons of Jupiter (the ones discovered by Galileo) satisfied this law. This fact was later used by Galileo as an argument in favour of Copernican system, since the moons were not orbiting Earth. |