A cubic function must have three intercepts, but they don't have to be different. Here we'll look at an example with three Real intercepts where two are the same, and another with three identical Real intercepts. . (1) Two Identical Intercepts y = x3 - 3x2 + 4 The y intercept is (0, 4) To find the x intercepts, we need to find one zero first, and divide to find the others. The possible zeros are +/- factors of 4, which are +/- 1, 2, and 4 By substituting into x3 - 3x2 + 4, we eventually find that -1 makes it equal zero. So a zero of the polynomial is -1. Now we know one factor is (x + 1) Divide (x3 - 3x2 + 4) by (x + 1) to get (x2 - 4x + 4) (x2 - 4x + 4) factors into (x - 2)(x - 2) So x3 - 3x2 + 4 = (x + 1)(x - 2)(x - 2) = (x + 1)(x - 2)2 This makes the three zeros -1, 2 and 2, and the x intercepts (-1, 0), (2, 0) and (2, 0)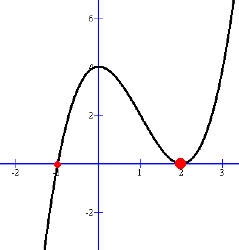 
Since the x3 first term is positive, the graph comes from the lower left quadrant. It then crosses at the first x intercept (-1, 0).After this, if it must eventually head up to the top right quadrant. When it loops down to the intercept (2, 0), it can't cross the axis, or there would have to be another intercept when it comes back up. So it must just touch at (2, 0) and turn back upwards. This happened because there were two identical x intercepts. When there are an even number of multiple intercepts the same, the graph touches the x intercept and turns around. (2) Three Identical Intercepts y = x3 - 6x2 + 12x - 8 The y intercept is (0, -8) The possible zeros are +/- 1, 2, 4, 8 By trial and error, we found that x = 2 makes the polynomial become zero. So one zero is 2. This makes one factor (x - 2) Dividing (x3 - 6x2 + 12x - 8) by (x - 2) gives (x2 - 4x + 4) x2 - 4x + 4 factors as (x - 2)(x - 2) So x3 - 6x2 + 12x - 8 = (x - 2)(x - 2)(x - 2) = (x - 2)3 All three zeros are at x = 2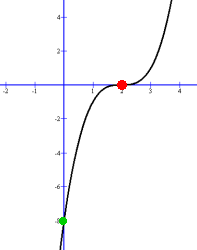 
Once again the graph comes from the lower left quadrant, and passes through the y intercept (0, -8) It passes through (2, 0) and continues upward to the right, to infinity. If there are an odd number of multiple intercepts the same, the graph passes through the x intercept. Note that there are no loops, but the graph changes the direction that it curves. This is called an 'inflection point', and is discussed in Math 31 (calculus). |