
Rational Zeros y = 8x3 + 12x2 - 2x - 3 The first coefficient is no longer 1, and it's not a common factor. We'll need the Rational Zero Theorem, which says that any zeros of the function must be: +/- factors of 3 (the constant term) factors of 8 (the first coefficient) The possible fractions that could be zeros are: +/- 1, 3 1, 2, 4, 8 Here are all the possible fractions listed: +/- 1/1, 1/2, 1/4, 1/8, 3/1, 3/2, 3/4, 3/8 simplifying: +/- 1, 1/2, 1/4, 1/8, 3, 3/2, 3/4, 3/8 We have sixteen values to substitute into 8x3 + 12x2 - 2x - 3, hoping to find the one value that is a zero. We can try the +/- integers first, and use decimal values for the others, but it's still a lot of work. In fact, we tried +1, -1, +3, and -3, and none worked. Eventually we found that substituting +1/2, or +0.5, made the polynomial work out to 0. So if 1/2 is a zero, the factor must be (2x - 1) Now we can divide 8x3 + 12x2 - 2x - 3 by (2x - 1) to get 4x2 + 8x + 3 Using decomposition, 4x2 + 8x + 3 = (2x + 1)(2x + 3) So 8x3 + 12x2 - 2x - 3 = (2x - 1)(2x + 1)(2x + 3) 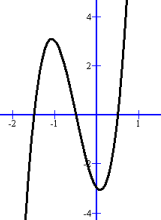
This makes the zeros 1/2, -1/2 and -3/2 Using decimals, the x intercepts are (0.5, 0), (-0.5, 0) and (-1.5, 0) The y intercept is (0, -3) You should also learn how to find zeros on a Ti83/Ti84 calculator, which is very quick, and useful when you aren't required to use algebra. In fact, using a calculator for things like this is a course requirement for Math 30. |