(1) Numerical Common Factor y = 2x3 + 4x2 - 2x - 4 The y intercept is (0, -4) To find the zeros, we factor the common factor first: 2x3 + 4x2 - 2x - 4 = 2(x3 + 2x2 - x - 2) This common factor affects the steepness of the graph, but has no effect on the zeros We can now find the zeros of x3 + 2x2 - x - 2 Possible zeros are +/- 1, 2 We found that -1 works So x = -1 is a zero, and (x + 1) is a factor Dividing x3 + 2x2 - x - 2 by (x + 1) gives x2 + x - 2 This factors into (x + 2)(x - 1)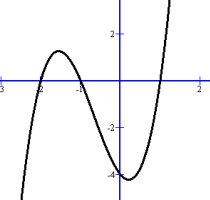 
So x3 + 2x2 - x - 2 = 2(x + 1)(x + 2)(x - 1) The zeros are -1, -2, and 1 the x intercepts are (-1, 0), (-2, 0) and (1, 0) The numerical common factor makes the graph steeper (and the y intercept numerically larger) but has no effect on the x intercepts. You may recognize a 'vertical stretch' from the Math 30 Transformations Unit (2) Variable Common Factor y = x3 + x2 - 6x The constant term is missing, so it must be 0. This makes the y intercept (0, 0) Here the common factor is x. We can factor it without having to use the Factor Theorem: y = x3 + x2 - 6x y = x(x2 + x - 6) y = x(x + 3)(x - 2)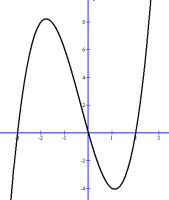 
If x(x + 3)(x - 2) = 0, then x can be 0, -3, or 2This makes the x intercepts (0, 0), (-3, 0) and (2, 0) We only have three points, but we can still make the graph. The effect of a variable common factor is to make one x intercept (0, 0), which is also the y intercept. Note once again that we don't really know the heights of the loops. |