Example 6: First Coefficient Negative


y = -x3 - 4x2 - 1x + 6

The end behaviours will be reversed:
As x gets increasingly large, the function will become increasingly more negative, so will go to negative infinity in the 4th quadrant. Conversely, when x has a very large negative value, the first coefficient negative will make the function become positive, meaning the left side of the graph will come from positive infinity. This corresponds to a vertical reflection, as discussed in the Transformations Unit.

y = -x3 - 4x2 - 1x + 6    We'll start by taking out a common factor of -1

y = -1(x3 + 4x2 + 1x - 6)

Now we'll find the x intercepts for
x3 + 4x2 + 1x - 6

Possible zeros are +/- 1, 2, 3, 6

x = 1 works, so a factor is (x - 1)

Dividing   x3 + 4x2 + 1x - 6   by   (x - 1)  gives  x2 + 5x + 6

x2 + 5x + 6  factors to  (x + 2)(x + 3)

So  y = -x3 - 4x2 - 1x + 6  =  -1(x - 1)(x + 2)(x + 3)

The x intercepts are (1, 0), (-2, 0) and (-3, 0) with y intercept (0, 6)

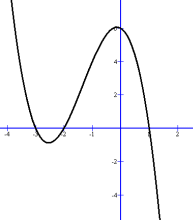Here's the graph; notice that the end behaviours are reversed.

Reminder: the heights of the loops are not determined. We're showing the actual graphs on these pages, but yours could look different. As long as the graph passes through the key points, and has the proper end behaviours, how tall you make the loops doesn't matter.

However, most Math 30 students will use a calculator to check the graph and correct the loop heights.




Finally, we have a few for you to try for practice, with answers.



Intro | Example 1 | Example 2 | Example 3 | Example 4 | Example 5 | Example 6 | Practice



Resources


Content, HTML, graphics & design by Bill Willis 2023