Cubic Functions ........................

Example 5: Irrational and Imaginary Intercepts

A cubic function must have one Real intercept. Before we look at a cubic function with imaginary intercepts, we need to examine what happens when the quadratic that results after dividing by the Real factor we found does not itself factor.

Two Irrational Intercepts

y = x³ - 7x² + 11x - 2

The y intercept is (0, -2)

We need to find one Real zero of x³ - 7x² + 11x - 2 which will be an integer

Possible zeros are +/- 1, 2

By trial and error, x = 2 makes the polynomial zero, so x = 2 is a zero, and (x - 2) is a factor.

Dividing (x³ - 7x² + 11x - 2) by (x - 2) results in (x² - 5x + 1)

x² - 5x + 1, however, does not factor. If there are zeros, they might be irrational:

We can find the zeros using the General Quadratic Formula:

For any quadraric equation ax² + bx + c = 0, the zeros are given by: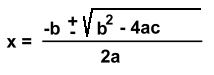

x² - 5x + 1 has a = 1, b = -5 and c = 1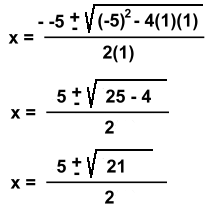

These irrational roots will give us irrational x intercepts.
Since we're looking for the graph, we'll evaluate the roots on a calculator, round them to 1 decimal place, and make the intercepts: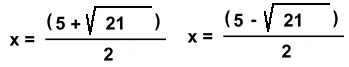

notice the brackets!

x = 4.8 and x = 0.2

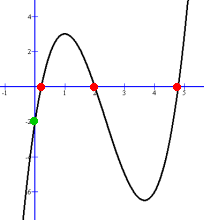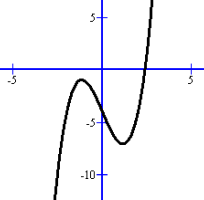
Factors are (x - 4.8) and (x - 0.2)

So y = x³ - 7x² + 11x - 2 = (x - 2)(x - 4.8)(x - 0.2)

The x intercepts are x = 2, x = 4.8 and x = 0.2
The y intercept is (0, -2)
The latter two are approximate, rounded to one decimal place, which is sufficient for graphing.
(Irrational zeros actually cannot be located exactly on an axis)

Two Imaginary Intercepts

y = x³ + 1x - 10

We know that there has to be one Real zero, and that it must be an integer.

The possible integral zeros are +/- 1, 2, 5, 10

x = 2 makes the polynomial zero, so x = 2 is a zero.

Dividing the polynomial by factor (x - 2) results in x² + 2x + 5, which again does not factor.

Using the G.Q. F. with a = 1, b = 2 and c = 5: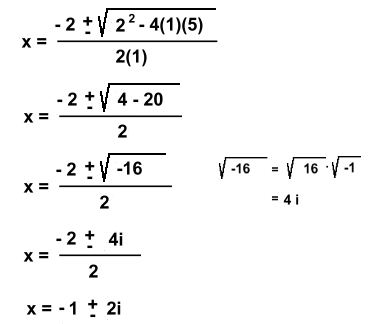

You can see that something strange happens.

As soon as we reach the line with the square root of -16, we can stop. Formerly we would have said this has no answer, but you have since learned that we really meant 'no Real answer'.

In fact, the square root of -16, and the two final solutions which we simplified, are Imaginary numbers, or more properly, elements of the set of Complex numbers.

Now the question is how these affect the graph!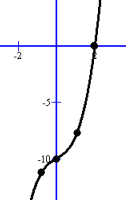

We have the y intercept (0, -10) and x intercept (2, 0).
To make the graph a little more accurate, we'll use the function to find
two more points: (1, -8) and (-1, -12).

Apparently the two imaginary intercepts don't make a detectable difference to the graph. In this example, we see the characteristic 'S' shape. Since there is one Real intercept, and no others are visible, we can surmise that the two others must be imaginary ones.

It's worth pointing out that a cubic function with two Imaginary intercepts can still have loops, as in the example here; the loops just can't touch or cross the x axis.