The problems on this page combine what you know about volume and surface formulas with your knowledge about how to simplify polynomials. You should try the problems on your own, and then use our solutions to check your answers.

Before looking at the problems on this page, you might want to review: as well as algebra involving:

Problem 1: Find the volume and surface area of the cube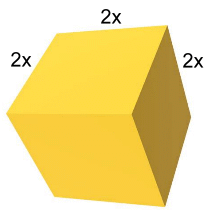

Volume = L3
V = L · L · L
V = (2x)(2x)(2x)
V = 8x3

Surface Area = 6·L2
SA = 6(2x)2
SA = 6(4x2)
SA = 24x2


Problem 2: Find the volume and surface area of the rectangular prism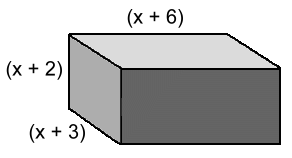


Volume = L·W·H
V = (x + 2)(x + 3)(x + 6)
V = (x + 2)(x2 + 9x + 18)
V = x3 + 9x2 + 18x + 2x2 + 18x + 36
V = x3 + 11x2 + 36x + 36

Surface Area = 2·L·W + 2·L·H + 2·W·H
SA = 2(x + 2)(x + 3) + 2 (x + 2)(x + 6) + 2(x + 3)(x + 6)
SA = 2(x2 + 5x + 6) + 2(x2 + 8x + 12) + 2(x2 + 9x + 18)
SA = 2x2 + 10x + 12 + 2x2 + 16x + 24 + 2x2 + 18x + 36
SA = 6x2 + 44x + 72


Problem 3: Find the volume and surface area of the cylinder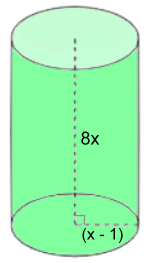

Volume = πr2H
V = π(x - 1)2(8x)
V = π(x2 - 2x + 1)(8x)
V = π(8x3 - 16x2 + 8x)

Surface Area = 2πr2 + 2πr·H
SA = 2π(x - 1)2 + 2π(x - 1)(8x)
SA = 2π(x2 - 2x + 1) + 2π(8x2 - 8x)
SA = π(2x2 - 4x + 2) + π(16x2 - 16x)
SA = π(2x2 - 4x + 2 + 16x2 - 16x)
SA = π(18x2 - 20x + 2)

           [Notice that it isn't necessary to multiply in the π]


Problem 4: Find the volume and surface area of the sphere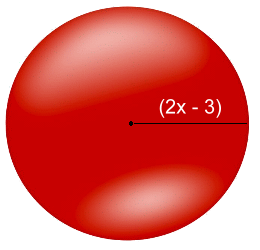

Volume = (4/3)πr3
V = (4/3)π(2x - 3)3
V = (4/3)π(2x - 3)(2x - 3)(2x - 3)
V = (4/3)π(2x - 3)(4x2 - 12x + 9)
V = (4/3)π(8x3 - 24x2 + 18x - 12x2 + 36x - 27)
V = (4/3)π(8x3 - 36x2 + 54x - 27)

[Here we leave both the fraction and the π unmultiplied]

Surface Area = 4πr2
SA = 4π(2x - 3)2
SA = 4π(4x2 - 12x + 9)
SA = π(16x2 - 48x + 36)


Resources


Content, HTML, graphics & design by Bill Willis 2024